题目内容
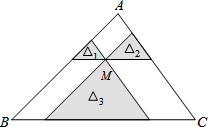如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是1、4、25．则△ABC的面积是考点：相似三角形的判定与性质
专题：
分析：根据平行可得出三个三角形相似，再由它们的面积比得出相似比，设其中一边为一求知数，然后计算出最大的三角形与最小的三角形的相似比，从而求面积比．
解答：过M作BC平行线交AB、AC于D、E，过M作AC平行线交AB、BC于F、H，过M作AB平行线交AC、BC于I、G，如图所示：
根据题意得，△1∽△2∽△3，
∵△1、△2的面积比为1：4，△1、△3的面积比为1：25，
∴它们边长比为1：2：5，
又∵四边形BDMG与四边形CEMH为平行四边形，
∴DM=BG，EM=CH，
设DM为x，
∴BC=（BG+GH+CH）=8x，
∴BC：DM=8：1，
∴S△ABC：S△FDM=64：1，
∴S△ABC=1×64=64
根据题意得，△1∽△2∽△3，
∵△1、△2的面积比为1：4，△1、△3的面积比为1：25，
∴它们边长比为1：2：5，
又∵四边形BDMG与四边形CEMH为平行四边形，
∴DM=BG，EM=CH，
设DM为x，
∴BC=（BG+GH+CH）=8x，
∴BC：DM=8：1，
∴S△ABC：S△FDM=64：1，
∴S△ABC=1×64=64
点评：本题考查了相似三角形的判定与性质，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
在某次数学测验中，随机抽取了10份试卷，其成绩如下：72，77，79，81，81，81，83，83，85，89，则这组数据的众数、中位数分别为（ ）
| A、81，82 |
| B、83，81 |
| C、81，81 |
| D、83，82 |
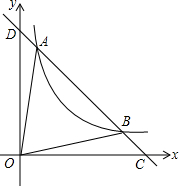如图，已知直线y1=ax+b与反比例函数y2=
请在方格纸上画出与AB、CD垂直的线段，并用字母表示．
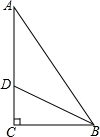如图，BD平分∠ABC，a=4，BD=
如图，AB是⊙O的直径，切线PC与AB延长线交于C，P为切点，点D是
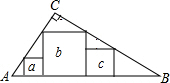如图，在Rt△ABC中（∠C=90°）放置边长分别为a、b、c的三个正方形，则a、b、c三者之间的数量关系为
分别指出如图中的同位角、内错角、同旁内角．