题目内容
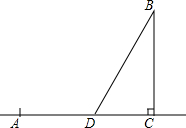由沿河城市A运货物到离河岸30km的地点B，按沿河距离计算，B离A的沿河距离AC是40km．如果水路运费是公路运费的一半，应怎样确定在河岸上的D，从B修一条公路到D，使由A到B的运费最省？考点：勾股定理的应用
专题：
分析：设AD=xkm，则CD=（40-x）km，根据勾股定理可知BD=
，再设水路运费a元/km，则公路运费为2a元/千米，由水路运费是公路运费的一半列出总费用的解析式，进而可得出结论．
| (40-x)2+302 |
解答：解：设AD=xkm，水路运费a元/km，则CD=（40-x）km，BD=
，公路运费为2a元/千米，
则总运费y=ax+2a
，
当x=40时，y=100a最小．即在离A40km即C处上岸运费最省．
| (40-x)2+302 |
则总运费y=ax+2a
| (40-x)2+302 |
当x=40时，y=100a最小．即在离A40km即C处上岸运费最省．
点评：本题考查的是勾股定理的应用，根据勾股定理列出BD的关系式是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在长为a，宽为b的大长方形中不重叠放置4个全等的小长方形，则阴影部分的周长之和为（ ）| A、2a | B、2b | C、4a | D、4b |
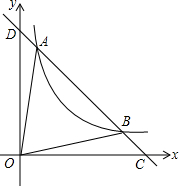如图，已知直线y1=ax+b与反比例函数y2=
如图，AB是⊙O的直径，CD切⊙O于C，OD⊥AB交AC于E，tan∠DEC=3，求sin∠D的值．
请在方格纸上画出与AB、CD垂直的线段，并用字母表示．
如图，AB是⊙O的直径，切线PC与AB延长线交于C，P为切点，点D是
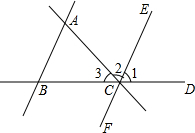如图，直线BD上有一点C，则：