题目内容
7.已知点A,B分别在x轴,y轴上,且OA=OB,P为动点,且PA⊥PB.(1)如图①,P在第一象限时,求∠OPA的度数.
(2)如图②,P在第四象限,求∠OPA的度数.
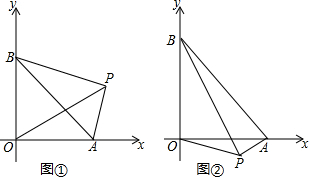
分析 (1)根据∠BOA=90°,∠APB=90°,可得O、B、P、A四点共圆,从而转换为求∠OBA 的度数;
(2)判断O、B、P、A四点共圆,根据“对角互补”,可得∠OPA的度数.
解答 解:(1)∵OA=OB,∠AOB=90°,
∴∠OBA=45°,
∵PA⊥PB,
∴∠APB=90°,
∵∠AOB+∠APB=180°,
∴O、B、P、A四点共圆,
∴∠OPA=∠OBA=45°;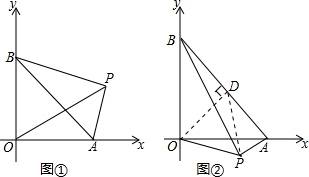 (2)过点O作OD⊥AB于点D,连接PD,
(2)过点O作OD⊥AB于点D,连接PD,
∵∠BOA=90°,BP⊥AP,
∴OD=BD=AD,
∴点D为AB的中点,
∴OD=DA=DB=PD,
∴O、B、P、A四点共圆,
∵∠OBA=45°,
∴∠OPA=135°.
点评 本题考查了四点共圆的知识,解答本题的关键思路清晰,判断四点共圆,利用四点共圆的性质求解.

练习册系列答案
相关题目
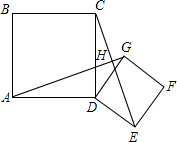 如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H
如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H  .
.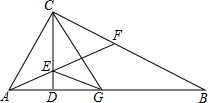 如图,已知CD是直角△ABC斜边上的高,∠BAC的平分线交CD于点E,交BC于点F,∠DCB的平分线交AB于点G.求证:EG∥BC.
如图,已知CD是直角△ABC斜边上的高,∠BAC的平分线交CD于点E,交BC于点F,∠DCB的平分线交AB于点G.求证:EG∥BC. 如图,EF∥GH∥BC,若AE=4,EG=2,GB=3,FH=1,则AF=2,AC=4.5.
如图,EF∥GH∥BC,若AE=4,EG=2,GB=3,FH=1,则AF=2,AC=4.5. 已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.
已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF. 如图,在?ABCD中,点E、F在BD上,且BF=DE,
如图,在?ABCD中,点E、F在BD上,且BF=DE,