��Ŀ����
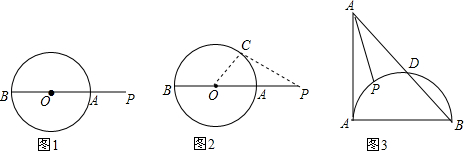
20���������龳����ͼ1��P�ǡ�O���һ�㣬ֱ��PO�ֱ�O�ڵ�A��B
С����Ϊ�߶�PA�ǵ�P����O�ϸ���ľ�������̵��߶Σ������������ǵģ��ڡ�O������ȡһ����ͬ�ڵ�A�ĵ�C������OC��CP������OP��OC+PC����OP-OC��PC����OA=OC��OP-OA��PC����PA��PC���Ӷ��ó��߶�PA�ǵ�P����O�ϸ���ľ�������̵��߶�
С����Ϊ��ͼ1�У��߶�PB�ǵ�P����O�ϸ���ľ���������߶Σ�����ΪС���˵����ȷ����˵������
��ֱ�����á�
��ͼ3����Rt��ABC�У���ACB=90�㣬AC=BC=2����BCΪֱ���İ�Բ��AB��D��P��$\widehat{CD}$�ϵ�һ�����㣬����AP����AP����Сֵ��$\sqrt{5}$-1
���������á�
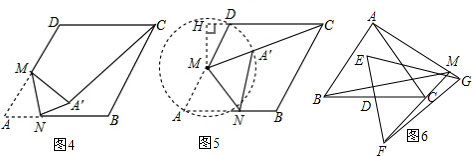
��ͼ4���ڱ߳�Ϊ4������ABCD�У���A=60�㣬M��AD�ߵ��е㣬N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C�������A��C���ȵ���Сֵ
�⣺���۵�֪A��M=AM����M��AD���е㣬�ɵ�MA=MA��=MD������A������ADΪֱ����Բ�ϣ���ͼ5���Ե�MΪԲ�ģ�MAΪ�뾶����M����M��MH��CD������ΪH���������ɱ���ĺ���������̣�
��������á�
��ͼ6����ABC����EFG���DZ߳�Ϊ4�ĵȱ������Σ���D�DZ�BC��EF���е㣬ֱ��AG��FC�ཻ�ڵ�M������EFG�Ƶ�D��תʱ�����߶�BM������Сֵ�����ֵ�ֱ���2$\sqrt{3}$-2��2$\sqrt{3}$+2��
���� �������龳�����ݡ������ε�����֮�ʹ��ڵ����ߡ�����֤����
��ֱ�����á��ҵ�BC���е�E������AE������Բ��P2���ڰ�Բ��ȡP1������AP1��EP1���ɼ���AP1+EP1��AE����AP2��AP����Сֵ���ٸ��ݹ��ɶ������AE�ij���Ȼ������뾶���ɣ�
���������á���������ó�A���λ�ã���������������Ǻ�����ϵ���A��C�ij����ɣ�
��������á�ȡAC���е�O������AD��DG��BO��OM����ͼ����֤��DAG�ס�DCF�����С�DAG=��DCF���Ӷ��ɵ�A��D��C��M�ĵ㹲Բ����������֮���߶���̿ɵ�BO��BM+OM����BM��BO-OM����M���߶�BO���Բ�Ľ��㴦ʱ���߶�BM��С��ֻ�����BO��OM��ֵ���Ϳɽ�����⣮
���  �⣺�������龳�����ͼ1����ԲO������ȡһ����ͬ�ڵ�B�ĵ�C������OC��OP��
�⣺�������龳�����ͼ1����ԲO������ȡһ����ͬ�ڵ�B�ĵ�C������OC��OP��
����OP+OC��PC��
��OB=OC�õ���OP+OB��PC����PB��PC��
�Ӷ��ó��߶�PB�ǵ�P��ԲO�ϸ���ľ���������߶Σ�
��ֱ�����á����ͼ2���ҵ�BC���е�E������AE������Բ��P2���ڰ�Բ��ȡP1������AP1��EP1��
�ɼ���AP1+EP1��AE��
��AP2��AP����Сֵ��
��AE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��P2E=1��
��AP2=$\sqrt{5}$-1��
�ʴ�Ϊ��$\sqrt{5}$-1��
���������á����ͼ3��ʾ����MA���Ƕ�ֵ��A��C����ȡ��Сֵʱ����A����MC��ʱ��
����M��MH��DC�ڵ�F��
���ڱ߳�Ϊ4������ABCD�У���A=60�㣬MΪAD�е㣬
��2MD=AD=CD=4����HDM=60�㣬
���HMD=30�㣬
��HD=$\frac{1}{2}$MD=1��
��HM=DM��cos30��=$\sqrt{3}$��
��MC=$\sqrt{H{M}^{2}+C{M}^{2}}$=2$\sqrt{7}$��
��A��C=MC-MA��=2$\sqrt{7}$-2��
��������á���AC���е�O������AD��DG��BO��OM�����ͼ4��
�ߡ�ABC����EFG���DZ߳�Ϊ4�ĵȱ������Σ���D�DZ�BC��EF���е㣬
��AD��BC��GD��EF��DA=DG��DC=DF��
���ADG=90��-��CDG=��FDC��$\frac{DA}{DC}$=$\frac{DG}{DF}$��
���DAG�ס�DCF��
���DAG=��DCF��
��A��D��C��M�ĵ㹲Բ��
�ٸ�������֮���߶���̿ɵã�BO��BM+OM����BM��BO-OM����M���߶�BO���Բ�Ľ��㴦ʱ���߶�BM��С��
��ʱ��BO=$\sqrt{B{C}^{2}-O{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$��OM=$\frac{1}{2}$AC=2��
��BM=BO-OM=2$\sqrt{3}$-2��
�ڸ�������֮���߶���̿ɵã�BM��BO+OM����M���߶�BO�ӳ������Բ�Ľ��㴦ʱ���߶�BM���
��ʱ��BO=$\sqrt{B{C}^{2}-O{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$��OM=$\frac{1}{2}$AC=2��
��BM=BO+OM=2$\sqrt{3}$+2��
�ʴ��ǣ�2$\sqrt{3}$-2��2$\sqrt{3}$+2��
���� �����ۺϿ����������ε����ʣ�ȫ�������ε��ж������ʣ�ֱ��������б���ϵ����ߵ���б�ߵ�һ������ʣ������ε����߹�ϵ��Բ�����ʣ����������á���ȷ����DH��Сʱ��H��λ���ǽ���ؼ�����������á����������M���˶��켣�ǽ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�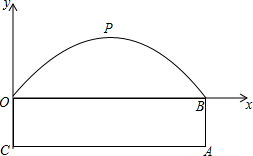 ��ͼ��ʾ��ij�����������������������߶ԳƵ�һ���ֺ;��ε�һ������ɣ����߶�Ϊ6�ף��ײ�����Ϊ12�ף�OC=3�ף�����ͼ����ƽ��ֱ������ϵ��
��ͼ��ʾ��ij�����������������������߶ԳƵ�һ���ֺ;��ε�һ������ɣ����߶�Ϊ6�ף��ײ�����Ϊ12�ף�OC=3�ף�����ͼ����ƽ��ֱ������ϵ��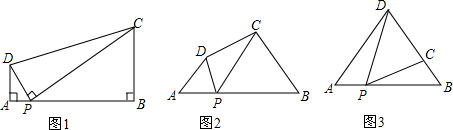
 ��ͼ��Rt��ABC�У���B=90�㣬AB=9��BC=6������ABC�۵���ʹA����BC���е�D�غϣ��ۺ�ΪMN�����߶�AN�ij����ڣ�������
��ͼ��Rt��ABC�У���B=90�㣬AB=9��BC=6������ABC�۵���ʹA����BC���е�D�غϣ��ۺ�ΪMN�����߶�AN�ij����ڣ�������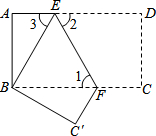 ��ͼ���ѳ�����ֽƬABCD��EF�۵���ʹ�õ�D���B�غϣ���C���ڵ�C���λ���ϣ�
��ͼ���ѳ�����ֽƬABCD��EF�۵���ʹ�õ�D���B�غϣ���C���ڵ�C���λ���ϣ�