题目内容
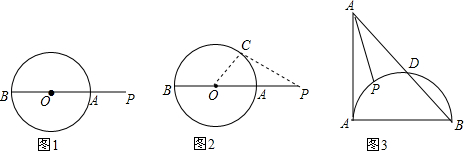
15. 如图,Rt△ABC中,∠B=90°,AB=9,BC=6,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段AN的长等于( )
如图,Rt△ABC中,∠B=90°,AB=9,BC=6,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段AN的长等于( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 设AN=x,由翻折的性质可知DN=AN=x,则BN=9-x,在Rt△DBN中利用勾股定理列方程求解即可.
解答 解:设AN=x,由翻折的性质可知DN=AN=x,则BN=9-x.
∵D是BC的中点,
∴BD=$\frac{1}{2}×6$=3.
在Rt△BDN中,由勾股定理得:ND2=NB2+BD2,即x2=(9-x)2+33,
解得:x=5.
AN=5.
故选:C.
点评 本题主要考查的是翻折的性质、勾股定理的应用,由翻折的性质得到DN=AN=x,BN=9-x,从而列出关于x的方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列各组线段中,长度成比例的是( )
| A. | 2cm、3cm、4cm、1cm | B. | 1.5cm、2.5cm、4.5cm、6.5cm | ||
| C. | 1.1cm、2.2cm、3.3cm、4.4cm | D. | 1cm、2cm、2cm、4cm |

 如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是($\sqrt{10}+1$,$\sqrt{10}+1$).
如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是($\sqrt{10}+1$,$\sqrt{10}+1$).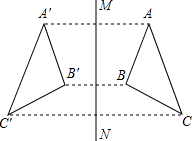 (1)如图,已知A、A′′′两点关于直线MN对称,则MN垂直平分AA′;
(1)如图,已知A、A′′′两点关于直线MN对称,则MN垂直平分AA′;