题目内容
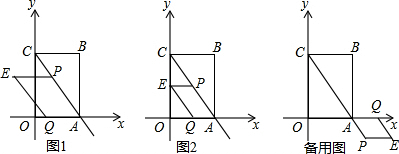
10. 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:①DE=DF;
②∠EDF=90°;
③四边形CEDF不可能为正方形;
④四边形CEDF的面积保持不变.
一定成立的结论有①②④(把你认为正确的序号都填上)
分析 ①连接CD,由SAS定理可证△CDF和△ADE全等,证明DE=DF;
②由△CDF和△ADE全等得到∠CDF=∠EDA,根据∠ADE+∠EDC=90°,得到∠EDF=90°;
③当E为AC中点,F为BC中点时,四边形CEDF为正方形;
④由割补法可知四边形CEDF的面积保持不变.
解答 解:①连接CD;
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCF}\\{AE=CF}\end{array}\right.$
∴△ADE≌△CDF(SAS),
∴ED=DF,①正确;
②∵△ADE≌△CDF,
∴∠CDF=∠EDA,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,②正确;
③当E、F分别为AC、BC中点时,DE⊥AC,DF⊥BC,又∠ACB=90°,
∴四边形CEDF是矩形,
∵CE=CF,
∴四边形CDFE是正方形,③错误;
④如图2,分别过点D,作DM⊥AC,DN⊥BC,于点M,N,
则DM=DN,
在Rt△DME和Rt△DNF中,
$\left\{\begin{array}{l}{DM=DN}\\{DE=DF}\end{array}\right.$,
∴Rt△DME≌Rt△DNF(HL),
∴四边形CEDF的面积等于正方形CMDN面积,故面积保持不变,④正确,
故答案为:①②④.
点评 此题主要考查了全等三角形的判定与性质以及正方形、等腰三角形、直角三角形性质等知识,根据图形利用割补法可知四边形CEDF的面积等于正方形CMDN面积是解题关键.

练习册系列答案
相关题目
20.若样本x1,x2,x3,x4,x5的而平均数为a,则样本3x1-6,3x2-6,3x3-6,3x4-6,3x5-6的平均数为( )
| A. | a | B. | 3a | C. | 3a-6 | D. | 3a+6 |
20.计算(-3a)2的结果是( )
| A. | 6a2 | B. | -9a2 | C. | 9a2 | D. | -6a2 |
 如图,菱形ABCD中,0是AC中点,EF经过点O,分别交AD,CB的延长线于点E,F.
如图,菱形ABCD中,0是AC中点,EF经过点O,分别交AD,CB的延长线于点E,F.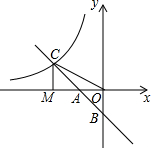 如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )