题目内容
12.如图,抛物线y=(x+1)2-4与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.(1)求A、C两点的坐标;
(2)抛物线的对称轴上存在一点P,使得△PBC的周长最小,求此时点P的坐标及最小周长;
(3)点M是抛物线上一动点,且在第三象限,当四边形AMCO的面积最大时,求出四边形AMCO的最大面积及此时点M的坐标.

分析 (1)分别令x=0,y=0即可解决问题.
(2)如图1中,连接AC交对称轴于P,此时△PBC周长最小.
(3)如图2中,设M(m,m2+2m-3),连接OM.根据S四边形AMCO=S△AOM+S△MOC构建二次函数,利用二次函数的性质解决问题.
解答 解:(1)令x=0,得y=-3,
∴点C坐标(0,-3).
令y=0则(x+1)2-4=0,解得x=-3或1,
∴点A坐标(-3,0),B(1,0),
∴A(-3,0),C(0,-3).
(2)如图1中,连接AC交对称轴于P,
∵PB=PA,
∴PB+PC=PB+PA,
∴此时PB+PC最短,△PBC的周长最短,
设直线AC解析式为y=kx+b则$\left\{\begin{array}{l}{b=-3}\\{-3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
∴直线AC解析式为y=-x-3,
∵对称轴x=-1,
∴点P坐标(-1,-2),
在Rt△AOC中,∵∠AOC=90°,OA=OC=3,
∴AC=3$\sqrt{2}$,
∵BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴△PBC周长的最小值为3$\sqrt{2}$+$\sqrt{10}$.
(3)如图2中,设M(m,m2+2m-3),连接OM.
∵S四边形AMCO=S△AOM+S△MOC=$\frac{1}{2}$×3×(-m2-2m+3)+$\frac{1}{2}$×3×(-m)=-$\frac{3}{2}$m2-$\frac{9}{2}$m+$\frac{9}{2}$=-$\frac{3}{2}$(m+$\frac{3}{2}$)2+$\frac{63}{8}$,
∵-$\frac{3}{2}$<0,
∴m=-$\frac{3}{2}$时,四边形AMCO面积最大,最大值为$\frac{63}{8}$,
此时点M(-$\frac{3}{2}$,-$\frac{15}{4}$).
点评 本题考查二次函数综合题、待定系数法、一次函数等知识,解题的关键是学会利用对称解决最短问题,学会构建二次函数解决最值问题.属于中考常考题型.

| A. | 无理数是无限不循环小数 | B. | 无理数是开不尽方的数 | ||
| C. | 无理数是含量有根号的数 | D. | 无理数是含有π的数 |

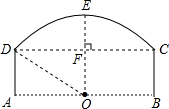 如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO.
如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO.