题目内容
4.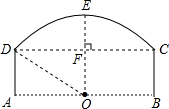 如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO.
如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO.
分析 先根据垂径定理求出DF的长,再由勾股定理即可得出结论.
解答 解:∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO-2,
在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO-2)2+42,解得:DO=5;
答:$\widehat{CD}$所在⊙O的半径DO为5m.
点评 本题考查的是垂径定理的应用,此类题中一般使用列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.

练习册系列答案
相关题目
15.下列图形中,对称轴的条数最少的图形是( )
| A. |  | B. |  | C. |  | D. |  |
14. 有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
 有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )| A. | -a | B. | 0 | C. | a+b | D. | b-a |


 画出如图的三视图.
画出如图的三视图.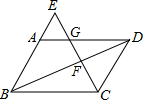 如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.
如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.