题目内容
7.已知,Rt△ABC中,∠C=90°,tanA=$\frac{1}{2}$,求sinA、cosA、sinB、cosB.分析 依题意知,sinA>0,cosA>0,根据tanA=$\frac{1}{2}$,sin2A+cos2A=1得到sinA、cosA的值;然后由“互余两角三角函数关系”求得sinB、cosB的值.
解答 解: ∵Rt△ABC中,∠C=90°,tanA=$\frac{1}{2}$,
∵Rt△ABC中,∠C=90°,tanA=$\frac{1}{2}$,
∴$\frac{sinA}{cosA}$=$\frac{1}{2}$,
∴sinA=2cosA,①
又sinA>0,cosA>0,sin2A+cos2A=1,②
联立①②得:sinA=$\frac{2\sqrt{5}}{5}$,cosA=$\frac{\sqrt{5}}{5}$.
又A+B=90°,
∴sinB=cosA=$\frac{\sqrt{5}}{5}$,cosB=sinA=$\frac{2\sqrt{5}}{5}$.
点评 本题考查了同角三角函数的关系,互余两角三角函数的关系,属于基础题,难度不大.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.下列图形中,对称轴的条数最少的图形是( )
| A. |  | B. |  | C. |  | D. |  |


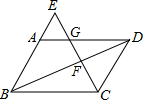 如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.
如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$. 如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.
如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.