题目内容
10.已知$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0,则$\frac{b+c}{a}$的值为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
分析 首先根据$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0,分别求出$\frac{b}{a}$、$\frac{c}{a}$的值各是多少;然后应用比例的性质,求出$\frac{b+c}{a}$的值为多少即可.
解答 解:∵$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0,
∴$\frac{b}{a}$=$\frac{5}{6}$,$\frac{c}{a}$=$\frac{4}{6}$,
∴$\frac{b+c}{a}$=$\frac{5+4}{6}$=$\frac{3}{2}$.
故选:B.
点评 此题主要考查了比例的性质和应用,要熟练掌握,解答此题的关键是分别求出$\frac{b}{a}$、$\frac{c}{a}$的值各是多少.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
1.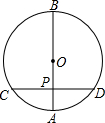 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
18. 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )| A. | 2,1,-2 | B. | -1,2,-2 | C. | -1,-2,2 | D. | -2,1,2 |
5.已知⊙O的半径是10,直线l是⊙O的切线,则圆心O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
15.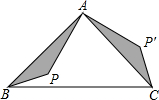 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
2.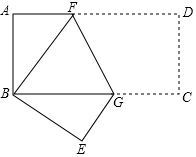 如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )
如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )
 如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )
如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )| A. | 2.5 | B. | 3 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
19.下列实数中无理数是( )
| A. | 0 | B. | 3 | C. | π | D. | $\sqrt{4}$ |
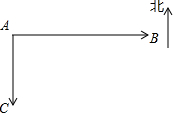 如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.
如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.