题目内容
19. 如图,已知DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于点O.求证:BE=CD,∠ACD=∠AEB.
如图,已知DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于点O.求证:BE=CD,∠ACD=∠AEB.
分析 根据SAS证明△ADC与△AEB全等,再利用全等三角形的性质证明即可.
解答 证明:∵DA⊥AB,EA⊥AC,
∴∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠EAB,
在△ADC与△AEB中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠EAB}\\{AE=AC}\end{array}\right.$,
∴△ADC≌△AEB(SAS),
∴BE=CD,∠ACD=∠AEB.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ADC与△AEB全等.

练习册系列答案
相关题目
8. 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )| A. | 12件 | B. | 8.625件 | C. | 8.5件 | D. | 9件 |

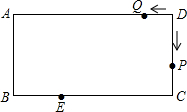 如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.
如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.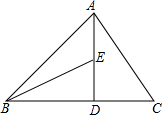 如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.
如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数. 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.
如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.