题目内容
18.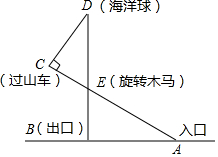 某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
分析 (1)在Rt△ABE中,利用三角函数即可直接求得BE的长;
(2)在Rt△CDE中,利用三角函数求得DE的长,然后利用DB=DE+EB求解.
解答 解:(1)∵在Rt△ABE中,∠BAE=30°,
∴BE=$\frac{1}{2}$AE=$\frac{1}{2}$×80=40(米);
(2)∵在Rt△ABE中,∠BAE=30°,
∴∠AEB=90°-30°=60°,
∴∠CED=∠AEB=60°,
∴在Rt△CDE中,DE=$\frac{CD}{sin∠CED}$≈$\frac{34}{\frac{1.7}{2}}$=40(米),
则BD=DE+BE=40+40=80(米).
点评 本题考查了解直角三角形,正确理解三角函数的定义,理解边角关系是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )
| A. | x1=0,x2=4 | B. | x1=-2,x2=6 | C. | x1=$\frac{3}{2}$,x2=$\frac{5}{2}$ | D. | x1=-4,x2=0 |
10.下列事件中,是确定事件的是( )
| A. | 三条线段围成一个三角形 | B. | 1小时等于60分钟 | ||
| C. | 度量三角形的内角和结果为360° | D. | 数轴上一点表示有理数 |
7. 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
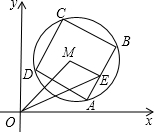 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.