题目内容
 如图,在△ABC中,D、E分别是边AC、BC上的点,若△ABD≌△EDB≌△EDC,求∠C的度数.
如图,在△ABC中,D、E分别是边AC、BC上的点,若△ABD≌△EDB≌△EDC,求∠C的度数.考点:全等三角形的性质
专题:
分析:根据全等三角形对应角相等可得∠ADB=∠BDE=∠CDE,然后求出∠CDE=60°,再根据直角三角形两锐角互余求解.
解答:解:∵△ABD≌△EDB≌△EDC,
∴∠ADB=∠BDE=∠CDE,
∴∠CDE=180°÷3=60°,
∴∠C=90°-60°=30°.
∴∠ADB=∠BDE=∠CDE,
∴∠CDE=180°÷3=60°,
∴∠C=90°-60°=30°.
点评:本题考查了全等三角形对应角相等的性质,熟记性质并准确识图找出对应角是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若点M在第三象限,且M到x轴,y轴的距离均为2,则点M关于x轴对称点的坐标为( )
| A、(2.1) |
| B、(-2,2) |
| C、(2,-2) |
| D、(-2,-2) |
若点A关于y轴的对称点是A(
,1),则点A的坐标为( )
| 1 |
| 2 |
A、(
| ||
B、(1,
| ||
C、(-
| ||
D、(
|
 如图,一根直立的旗杆高8米,一阵大风吹过,旗杆从点C处这段,顶部(B)着地,离旗杆底部(A)4米,工人在修复的过程中,发现在折断点C的下方1.25米D处,有一明显裂痕,若下次大风将旗杆从D处吹断,则距离杆脚周围多大范围内有被砸伤的危险?
如图,一根直立的旗杆高8米,一阵大风吹过,旗杆从点C处这段,顶部(B)着地,离旗杆底部(A)4米,工人在修复的过程中,发现在折断点C的下方1.25米D处,有一明显裂痕,若下次大风将旗杆从D处吹断,则距离杆脚周围多大范围内有被砸伤的危险?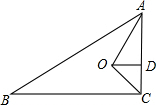 如图,在△ABC中,∠ACB=90°,AO、GO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.
如图,在△ABC中,∠ACB=90°,AO、GO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.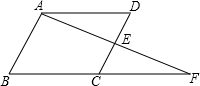 如图,在平行四边形ABCD中,E是CD的中点,连接AE并延长交BC的延长线于点F.
如图,在平行四边形ABCD中,E是CD的中点,连接AE并延长交BC的延长线于点F.