题目内容
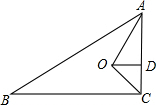 如图,在△ABC中,∠ACB=90°,AO、GO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.
如图,在△ABC中,∠ACB=90°,AO、GO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.考点:角平分线的性质,勾股定理
专题:
分析:连接OB,过O作OE⊥AB于E,OF⊥BC于F,求出OE=OD=OF,设OD=OE=OF=R,根据勾股定理求出AC长,根据三角形的面积得出S△ABC=S△ABO+S△ACO+S△BCO,代入求出R即可.
解答:解:连接OB,过O作OE⊥AB于E,OF⊥BC于F,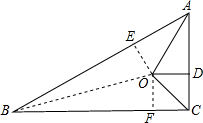
∵AO平分∠BAC,CO平分∠ACB,OE⊥AB,OF⊥BC,OD⊥AC,
∴OE=OD=OF,
设OE=OF=OD=R,
在△ABC中,∠ACB=90°,AB=10,BC=8,由勾股定理得:AC=6,
∵S△ABC=S△ABO+S△ACO+S△BCO,
∴
AC×BC=
AB×OE+
AC×OD+
BC×OF,
∴6×8=6R+8R+10R,
解得:OD=R=2.
∴OD的长为2.

∵AO平分∠BAC,CO平分∠ACB,OE⊥AB,OF⊥BC,OD⊥AC,
∴OE=OD=OF,
设OE=OF=OD=R,
在△ABC中,∠ACB=90°,AB=10,BC=8,由勾股定理得:AC=6,
∵S△ABC=S△ABO+S△ACO+S△BCO,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴6×8=6R+8R+10R,
解得:OD=R=2.
∴OD的长为2.
点评:本题考查了角平分线性质和勾股定理的应用,关键是得出关于R的一元一次方程,题目比较典型,主要培养学生的计算能力.

练习册系列答案
相关题目
 如图,在△ABC中,D、E分别是边AC、BC上的点,若△ABD≌△EDB≌△EDC,求∠C的度数.
如图,在△ABC中,D、E分别是边AC、BC上的点,若△ABD≌△EDB≌△EDC,求∠C的度数.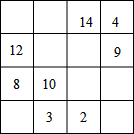 将1~16这16个整数填入4×4的正方形表格中,使得每行、每列、每条对角线上四个数之和都相等,如图所示,恰有8个小方格中填的数被一个淘气的小朋友擦掉了,请你将擦掉的这8个数设法恢复出来.
将1~16这16个整数填入4×4的正方形表格中,使得每行、每列、每条对角线上四个数之和都相等,如图所示,恰有8个小方格中填的数被一个淘气的小朋友擦掉了,请你将擦掉的这8个数设法恢复出来.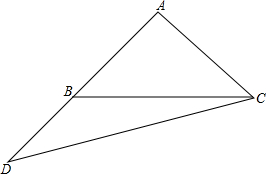 如图,在△ABC中,AB=AC,∠ABC=40°,延长AB到D,使得AD=BC,连结CD,求∠D的度数.
如图,在△ABC中,AB=AC,∠ABC=40°,延长AB到D,使得AD=BC,连结CD,求∠D的度数.