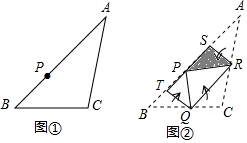图①为三角形纸片ABC.AB上有一点P.已知将A.B.C往内折至P时.出现折线SR.TQ.QR.其中Q.R.S.T四点分别在BC.AC.AP.BP上.如图②所示.若△ABC.四边形PTQR的面积分别为20.8.则阴影部分面积为( )A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

3．

图①为三角形纸片ABC，AB上有一点P，已知将A、B、C往内折至P时，出现折线SR、TQ、QR，其中Q、R、S、T四点分别在BC、AC、AP、BP上，如图②所示，若△ABC、四边形PTQR的面积分别为20、8，则阴影部分面积为（　　）

A．

B．

C．

D．

分析根据折叠，知△BTQ的面积和△PTQ的面积相等，△CQR和△PQR的面积相等，△ASR的面积和△PSR的面积相等，结合已知△ABC、四边形PTQR的面积分别为20、8，即可求解．

解答解：根据题意，得△BTQ的面积和△PTQ的面积相等，△CQR和△PQR的面积相等，△ASR的面积和△PSR的面积相等，
又∵△ABC、四边形PTQR的面积分别为20、8，
∴△PRS面积等于（20-8×2）÷2=2．
故选B．

点评本题主要考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变．

练习册系列答案

本土教辅名校学案黄冈期末全程特训卷系列答案

易学练系列答案

名师点拨期末冲刺满分卷系列答案

14．把一张正方形纸片，连续对折三次，得到的图形面积是这个正方形面积的（　　）

11．已知一个样本-1，0，2，x，3，它们的平均数是2，则x=6，方差S²=6．

18．

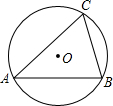如图，锐角△ABC是⊙O的内接三角形，若AC=17cm，BC=10cm，⊙O的直径是21.25cm，则△ABC的面积是84cm²．

8．阅读材料，解答下列问题：
例：当a＞0时，如a=5，则|a|=|5|=5，故此时a的绝对值是它本身；当a=0时，|a|=0，故此时a的绝对值是0；当a＜0时，如a=-5，则|a|=|-5|=-（-5），故此时a的绝对值是它的相反数．综上所述，一个数的绝对值要分三种情况，即：|a|=$\left\{\begin{array}{l}{a（a＞0）}\\{0（a=0）}\\{-a（a＜0）}\end{array}\right.$，这种分析方法渗透了数学中的分类讨论思想．
（1）请仿照例中的分类讨论，分析$\sqrt{{a}^{2}}$的各种化简后的情况；
（2）猜想$\sqrt{{a}^{2}}$与|a|的大小关系；
（3）当1＜x＜2时，试化简|x+1|+$\sqrt{（x-2）^{2}}$．

15．下列各对近似数中，精确度一样的是（　　）

12．已知二次函数y=x²-4x-5，若y＞0，则（　　）

13．

填写下面证明过程中的推理依据：
已知：如图，AB∥CD，BE平分∠ABC，CF平分∠BCD．求证：∠1=∠2
证明：∵AB∥CD （已知）
∴∠ABC=∠BCD（两直线平行，内错角相等）
∵BE平分∠ABC，CF平分∠BCD （已知）
∴∠1=$\frac{1}{2}$∠ABC，（角平分线的定义）
∠2=$\frac{1}{2}$∠BCD．（角平分线的定义）
∴∠1=∠2．（等量代换）

试题分类