题目内容
14.把一张正方形纸片,连续对折三次,得到的图形面积是这个正方形面积的( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
分析 把这个正方形纸片对折一次,把图形平均分成2份,对折两次,图形平均分成四份,对折3次,把图形平均分成8份,即可得出结论.
解答 解:1÷8=$\frac{1}{8}$,
即:所得的图形面积是原图形面积的$\frac{1}{8}$,
故选D.
点评 此题是折叠问题,主要考查了折叠的性质,解本题的关键是明确对折三次把正方形平均分成8份.

练习册系列答案
相关题目
9.如图,在数轴上放置一个长方形块,长方形的长为$\frac{3}{4}$,宽为$\frac{1}{3}$.此时将长方形沿数轴正方向做顺时针的翻动.长方形所在的初始位置如图中实线所示,沿A点(如图所示)做数轴的垂线,在数轴上所对应的数字是1.
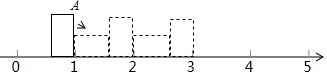
(1)第3次翻动长方形块后,A点在数轴上所对应的数字表示是$\frac{25}{12}$
(2)第8次翻动长方形块后,A点在数轴上所对应的数字表示是5$\frac{1}{3}$
(3)第101次翻动长方形块后,A点在数轴上所对应的数字表示是55$\frac{11}{12}$.

| 翻动次数 | A点在数轴上对应的数字 |
| 1 | 1+$\frac{3}{4}$ |
| 2 | 1+$\frac{3}{4}$+0 |
| 3 | |
| 4 |
(2)第8次翻动长方形块后,A点在数轴上所对应的数字表示是5$\frac{1}{3}$
(3)第101次翻动长方形块后,A点在数轴上所对应的数字表示是55$\frac{11}{12}$.
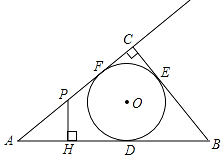 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H. 如图,⊙O的半径为$\sqrt{2}$,圆周角∠BAC=135°,求BC的长.
如图,⊙O的半径为$\sqrt{2}$,圆周角∠BAC=135°,求BC的长.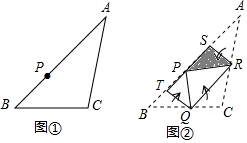 图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、QR,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为20、8,则阴影部分面积为( )
图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、QR,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为20、8,则阴影部分面积为( ) 如图,A、B分别为y=x2图象上的两点,且AB⊥y轴,AB=6,
如图,A、B分别为y=x2图象上的两点,且AB⊥y轴,AB=6,