题目内容
18. 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:| △ABC | A(a,0) | B(3,0) | C(5,5) |
| △A1B1C1 | A1(-3,2) | B1(-1,b) | C1(c,7) |
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是5.
分析 (1)根据点B横坐标的变化求出向左平移的距离,根据点C纵坐标的变化得出向上平移的距离即可;
(2)在坐标系内描出各点,再画出△ABC及△A1B1C1即可;
(3)矩形的面积减去两个顶点上三角形的面积即可.
解答  解:(1)∵B(3,0),B1(-1,b),
解:(1)∵B(3,0),B1(-1,b),
∴向左平移的距离=3+1=4,
∴a-4=-3,解得a=1,
5-c=4,解得c=1;
∵C(5,5),C1(c,7),
∴向上平移的距离=7-5=2,
∴n=0+2=2.
故答案为:1,2,1;
(2)如图△ABC及△A1B1C1即为所求;
(3)由图可知,S△A1B1C1=4×5-$\frac{1}{2}$×4×5-$\frac{1}{2}$×2×4=5.
故答案为:5.
点评 本题考查的是作图-平移变换,先根据题意得出图形平移的方向,再根据图形平移不变性的性质求解是解答此题的关键.

练习册系列答案
相关题目
8.根据下列表格中的数值,判断方程ax2+bx+c=0(a,b为常数)根的情况( )
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| ax2+bx+c | … | -3 | 2 | 3 | 0 | -7 | … |
| A. | 有两个不相等实根 | B. | 有两个相等实根 | ||
| C. | 只有一个实根 | D. | 无实根 |
9.方程x+3y=5与下列哪个方程组合,使得方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$( )
| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
3.计算$\sqrt{36}$的结果是( )
| A. | 6 | B. | ±6 | C. | -6 | D. | 36 |
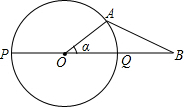 如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论:
如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论: 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°. 如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
如图,三条直线交于同一点,则∠1+∠2+∠3=180°.