题目内容
10.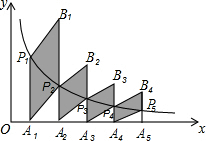 如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…,An,连接A1P2,A2P3,…,AnPn+1,…,以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,其面积为S1,以A2P2,A2P3为一组邻边作平行四边形A2P2B2P3,其面积为S2,…,以AnPn,AnPn+1为一组邻边作平行四边形AnPnBnPn+1,其面积为Sn,若S1+S2+…+Sn>8,则n的最小值为( )
如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…,An,连接A1P2,A2P3,…,AnPn+1,…,以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,其面积为S1,以A2P2,A2P3为一组邻边作平行四边形A2P2B2P3,其面积为S2,…,以AnPn,AnPn+1为一组邻边作平行四边形AnPnBnPn+1,其面积为Sn,若S1+S2+…+Sn>8,则n的最小值为( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
分析 根据反比例函数图象上点的坐标特征以及平行四边形的面积,即可得出S1=3、S2=$\frac{3}{2}$、S3=1、…、Sn=$\frac{3}{n}$,结合S1+S2+…+Sn>8,即可找出n≥8,此题得解.
解答 解:∵P1(1,y1),P2(2,y2),…,Pn(n,yn),
∴P1A1=y1=3,P2A2=y2=$\frac{3}{2}$,P3A3=y3=1,…,PnAn=yn=$\frac{3}{n}$,
∴S1=3,S2=$\frac{3}{2}$,S3=1,…,Sn=$\frac{3}{n}$.
∵S1+S2+…+Sn>8,
∴1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>$\frac{8}{3}$.
∵当n=7时,1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{7}$=$\frac{1089}{420}$<$\frac{1120}{420}$=$\frac{8}{3}$;当n=8时,1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{8}$=$\frac{2283}{840}$>$\frac{2240}{840}$=$\frac{8}{3}$,
∴若S1+S2+…+Sn>8,则n的最小值为8.
故选B.
点评 本题考查了平行四边形的面积以及反比例函数图象上点的坐标特征,根据反比例函数图象上点的坐标特征以及平行四边形的面积,找出Sn=$\frac{3}{n}$是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).
已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).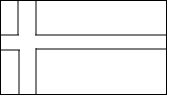 某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积560m2.
某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积560m2. 如图,△ABC中,∠A=60°,∠B=80°,CD是∠ACB的平分线,DE⊥AC于点E,EF∥CD交AB于F,则∠DEF的度数为70°.
如图,△ABC中,∠A=60°,∠B=80°,CD是∠ACB的平分线,DE⊥AC于点E,EF∥CD交AB于F,则∠DEF的度数为70°.