题目内容
5．已知关于x、y的方程组$\left\{\begin{array}{l}{2x+5y=3k}\\{5x+2y=4-k}\end{array}\right.$的解满足不等式x-y＞1，求满足条件的k的取值范围．分析 将两方程相减得出x-y=$\frac{4-4k}{3}$，由x-y＞1得$\frac{4-4k}{3}$＞1，解之即可．
解答 解：$\left\{\begin{array}{l}{2x+5y=3k}&{①}\\{5x+2y=4-k}&{②}\end{array}\right.$，
②-①，得：3x-3y=4-4k，
即x-y=$\frac{4-4k}{3}$，
∵x-y＞1，
∴$\frac{4-4k}{3}$＞1，
解得：k＜$\frac{1}{4}$．
点评 本题主要考查解二元一次方程组和一元一次不等式的能力，根据方程的特点简便得出关于k的不等式是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE，连接BG、DE．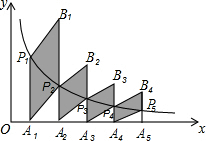
如图，分别过反比例函数y=$\frac{3}{x}$图象上的点P1（1，y1），P2（2，y2），…，Pn（n，yn）作x轴的垂线，垂足分别为A1，A2，…，An，连接A1P2，A2P3，…，AnPn+1，…，以A1P1，A1P2为一组邻边作平行四边形A1P1B1P2，其面积为S1，以A2P2，A2P3为一组邻边作平行四边形A2P2B2P3，其面积为S2，…，以AnPn，AnPn+1为一组邻边作平行四边形AnPnBnPn+1，其面积为Sn，若S1+S2+…+Sn＞8，则n的最小值为（ ）
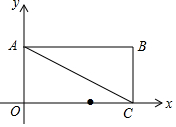如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=1，OC=2，点D在边OC上且OD=1.25．