题目内容
 如图是某座拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥与水面相接处的跨度AB为10m,桥洞上沿与水面的最大距离是5m.
如图是某座拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥与水面相接处的跨度AB为10m,桥洞上沿与水面的最大距离是5m.(1)以AB的中点O为原点,AB所在直线为x轴,建立平面直角坐标系(1个单位长度表示1m),求桥洞上沿所在抛物线对应的函数表达式;
(2)若水面上涨1m,求此时的水面宽CD.
考点:二次函数的应用
专题:
分析:(1)根据函数图象假设出函数解析式,得出图象上点的坐标,进而求出函数解析式;
(2)利用y=1时,求出x的值,进而得出答案.
(2)利用y=1时,求出x的值,进而得出答案.
解答:解:(1)由题意可得:设抛物线解析式为:y=ax2+5,B点坐标为:(5,0),
则0=25a+5,
解得:a=-
.
故桥洞上沿所在抛物线对应的函数表达式为:y=-
x2+5;
(2)由题意可得:y=1时,1=-
x2+5,
解得:x1=2
,x2=-2
,
故此时的水面宽CD为:2
+2
=4
.
则0=25a+5,
解得:a=-
| 1 |
| 5 |
故桥洞上沿所在抛物线对应的函数表达式为:y=-
| 1 |
| 5 |
(2)由题意可得:y=1时,1=-
| 1 |
| 5 |
解得:x1=2
| 5 |
| 5 |
故此时的水面宽CD为:2
| 5 |
| 5 |
| 5 |
点评:此题主要考查了二次函数的应用,根据题意得出函数关系式是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
-0.5的相反数是( )
| A、0.5 | B、-0.5 |
| C、-2 | D、2 |
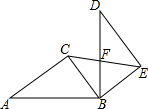 如图,在RT△ABC中,∠ACB=90°AB=10,BC=6.将RT△ABC绕点B旋转90°至△DBE的位置,连接EC交BD于F,则CF:FE的值是( )
如图,在RT△ABC中,∠ACB=90°AB=10,BC=6.将RT△ABC绕点B旋转90°至△DBE的位置,连接EC交BD于F,则CF:FE的值是( )| A、3:4 | B、3:5 |
| C、4:3 | D、5:3 |
 如图,方格纸中每个小方格的边长为1,在方格纸内画一个面积为6.5的等腰直角三角形.要求:所画三角形的顶点在小方格的顶点上.
如图,方格纸中每个小方格的边长为1,在方格纸内画一个面积为6.5的等腰直角三角形.要求:所画三角形的顶点在小方格的顶点上.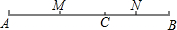 如图,点C在线段AB上,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,点M、N分别是AC、BC的中点. 如图,E,F分别是等腰△ABC的腰AB,AC的中点.
如图,E,F分别是等腰△ABC的腰AB,AC的中点.
 如图,AB是⊙O的直径,PAC是⊙O的割线,∠PAB的平分线与⊙0交于D,DE⊥PC于E.
如图,AB是⊙O的直径,PAC是⊙O的割线,∠PAB的平分线与⊙0交于D,DE⊥PC于E. 如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.