Question

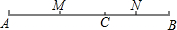如图，点C在线段AB上，点M、N分别是AC、BC的中点．
（1）若AC=8cm，CB=6cm，求线段MN的长；
（2）若C为线段AB上任一点，满足AC+CB=acm，其它条件不变，求MN的长（直接写出结论即可）；
（3）若C在线段AB的延长线上，且满足AC-BC=bcm，M、N分别为AC、BC的中点，求MN的长度．

Answer 1

考点：两点间的距离,一元一次方程的应用

专题：

分析：（1）、（2）根据线段的中点的性质，可得MC、NC的长，再根据线段的和差，可得答案．
（3）根据线段中点得出CM=

1

2

AC，CN=

1

2

BC，求出MN=CM-CN=

1

2

AC-

1

2

BC，代入即可得出答案．

解答：解：（1）∵点M、N分别是AC、BC的中点，
∴MC=

1

2

AC，NC=

1

2

CB，
又∵AC=8cm，BC=6cm，
∴MN=MC+NC=

1

2

（AC+BC）=7cm．

（2）由（1）知，MN=MC+NC=

1

2

（AC+BC）．
∵AC+CB=acm，
∴MN=

a

2

m；

（3）如图：

MN=

1

2

b，
理由是：∵点M、N分别是AC、BC的中点，AC-CB=bcm，
∴CM=

1

2

AC，CN=

1

2

BC，
∴MN=CM-CN=

1

2

AC-

1

2

BC=

1

2

（AC-BC）=

1

2

bcm，
即线段MN的长是

1

2

bcm．

点评：本题考查了线段中点定义和两点间的距离的应用，主要考查学生的计算能力，本题比较典型，是一道比较好且比较容易出错的题目．