题目内容
 如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.(1)求△COP的面积;
(2)求点A的坐标;
(3)求直线BD的函数关系式.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)由A、B关于y轴对称的两点得到OA=OB,则S△POB=S△AOP=6,根据三角形面积公式得到
•3•OB=6,解得OB=4,即可得到B点坐标,再利用待定系数法求出直线BP的解析式,然后确定直线与y轴的交点D的坐标,再利用三角形面积公式求解;
(2)利用A、B关于y轴对称的两点确定A点坐标;
(3)由(1)得直线BD的解析式.
| 1 |
| 2 |
(2)利用A、B关于y轴对称的两点确定A点坐标;
(3)由(1)得直线BD的解析式.
解答:解:(1)∵A、B关于y轴对称的两点,
∴OA=OB,
∴S△POB=S△AOP=6.
∴
•3•OB=6,解得OB=4,
∴B点坐标为(4,0),
式直线PB的解析式为y=kx+b,
把P(2,3)、B(4,0)分别代入得
,解得
,
∴直线PB的解析式为y=-
x+6,
当x=0时,y=-
x+6=6,则D点坐标为(0,6),
∴△COP的面积=
×2×(6-2)=4;
(2)∵A、B关于y轴对称的两点,
∴A点坐标为(-4,0);
(3)由(1)得直线BD的解析式为y=-
x+6.
∴OA=OB,
∴S△POB=S△AOP=6.
∴
| 1 |
| 2 |
∴B点坐标为(4,0),
式直线PB的解析式为y=kx+b,
把P(2,3)、B(4,0)分别代入得
|
|
∴直线PB的解析式为y=-
| 3 |
| 2 |
当x=0时,y=-
| 3 |
| 2 |
∴△COP的面积=
| 1 |
| 2 |
(2)∵A、B关于y轴对称的两点,
∴A点坐标为(-4,0);
(3)由(1)得直线BD的解析式为y=-
| 3 |
| 2 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果△ABC∽△DEF,其相似比为3:1,且△ABC的周长为27,则△DEF的周长为( )
| A、9 | B、18 | C、27 | D、81 |
 如图是某座拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥与水面相接处的跨度AB为10m,桥洞上沿与水面的最大距离是5m.
如图是某座拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥与水面相接处的跨度AB为10m,桥洞上沿与水面的最大距离是5m.
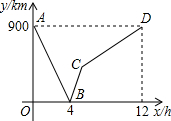 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: 如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题:
如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题: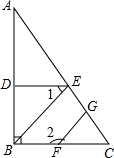 如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由.
如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由. 在△ABC中,∠B=∠C,点D在BC上,点E在AC上,∠BAD=2∠CDE,那么∠ADE与∠AED相等吗?为什么?
在△ABC中,∠B=∠C,点D在BC上,点E在AC上,∠BAD=2∠CDE,那么∠ADE与∠AED相等吗?为什么? 如图,在直角坐标系中,A、B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中A为直角顶点,P为斜边BC的中点,则下列说法中正确的是
如图,在直角坐标系中,A、B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中A为直角顶点,P为斜边BC的中点,则下列说法中正确的是