题目内容
17.用换元法解方程$\frac{3x}{{x}^{2}-1}$+$\frac{{x}^{2}-1}{x}$=$\frac{5}{2}$,设y=$\frac{x}{{{x^2}-1}}$,那么原方程化为关于y的整式方程是3y+$\frac{1}{y}$=$\frac{5}{2}$.分析 根据y=$\frac{x}{{{x^2}-1}}$,将方程变形即可.
解答 解:根据题意得:3y+$\frac{1}{y}$=$\frac{5}{2}$,
故答案为:3y+$\frac{1}{y}$=$\frac{5}{2}$
点评 此题考查了换元法解分式方程,利用了整体的思想,将方程进行适当的变形是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如图所示的整式化简过程,对于所列的每一步运算,依据错误的是( )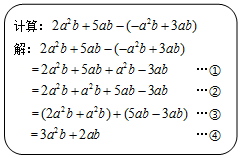
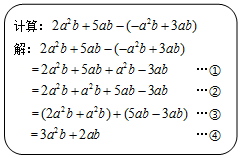
| A. | ①:去括号法则 | B. | ②:加法交换律 | ||
| C. | ③:等式的基本性质 | D. | ④:合并同类项法则 |
5.下列方程中,是一元一次方程的是( )
| A. | $\frac{2x-2}{3}$=$\frac{5-x}{6}$+$\frac{1}{2}$ | B. | $\frac{1}{2x}$=-$\frac{1}{x}$+4 | C. | 2x2-3x+1=0 | D. | x+21=y-13. |
10.在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在下列关系中,不属于直角三角形的是( )
| A. | b2=a2-c2 | B. | a:b:c=3:4:5 | C. | ∠A-∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
 请把下列解题过程补充完整并在括号中注明理由.如图,EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD.
请把下列解题过程补充完整并在括号中注明理由.如图,EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD.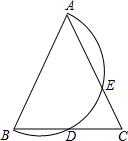 等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.
等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.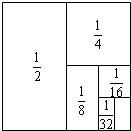 如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.
如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.