题目内容
5.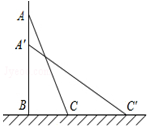 一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.9米到A′,那么梯子的底端在水平方向滑动了几米?
分析 (1)利用勾股定理可以得出梯子的顶端距离地面的高度;
(2)求出A′B=1.6(米),由勾股定理求出BC′≈1.9(米),得出CC′的长即可.
解答 解:(1)根据勾股定理:AB=$\sqrt{2.{5}^{2}-0.{7}^{2}}$=2.4(米),
答:这个梯子的顶端距地面有2.4米;
(2)根据题意得:A′B=2.5-0.9=1.6(米),
∴BC′=$\sqrt{2.{5}^{2}-1.{6}^{2}}$≈1.9(米),
∴CC′=BC′-BC=1.9-0.7=1.2(米);
答:如果梯子的顶端下滑了0.9米到A′,那么梯子的底端在水平方向滑动了约1.2米.
点评 本题考查了勾股定理在实际生活中的运用,考查了直角三角形中勾股定理的运用,本题中正确的使用勾股定理求AB的长度是解题的关键.

练习册系列答案
相关题目
15.下列结论中错误的是( )
| A. | 三角形的内角和等于180° | |
| B. | 三角形的外角和小于四边形的外角和 | |
| C. | 五边形的内角和等于540° | |
| D. | 正六边形的一个内角等于120° |
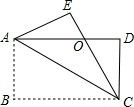 如图,把一个长方形的纸沿对角线折叠,使点B落在点E处,CE交AD于点O,若CE平分∠ACD,且AB=2$\sqrt{3}$,BC=6,则S△AOC=4$\sqrt{3}$.
如图,把一个长方形的纸沿对角线折叠,使点B落在点E处,CE交AD于点O,若CE平分∠ACD,且AB=2$\sqrt{3}$,BC=6,则S△AOC=4$\sqrt{3}$.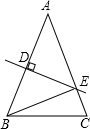 如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.△BCE的周长是53cm,则BC=21cm.
如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.△BCE的周长是53cm,则BC=21cm. 如图,△ABC中,∠B=35°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC的延长线上的D点处,求∠BDE的度数.
如图,△ABC中,∠B=35°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC的延长线上的D点处,求∠BDE的度数.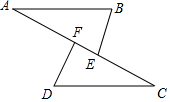 点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.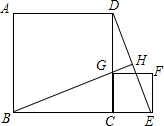 已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:
已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证: