题目内容
2.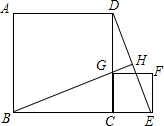 已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:
已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:(1)△BCG≌△DCE;
(2)HB⊥DE.
分析 根据正方形的边的性质和直角可通过SAS判定△BCG≌△DCE,从而利用全等的性质得到∠BHD=90°即BH⊥DE;
解答 证明:(1)在正方形ABCD中,∠BCG=90°,BC=CD
在正方形GCEF中,∠DCE=90°,CG=CE
在△BCG和△DCE中,$\left\{\begin{array}{l}{BC=DC\\;}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$
∴△BCG≌△DCE(SAS)
(2)∵△BCG≌△DCE,
∴∠1=∠2∵∠2+∠DEC=90°
∴∠1+∠DEC=90°
∴∠BHD=90°
∴BH⊥DE;
点评 此题主要考查正方形的性质,全等三角形的判定等几何知识.关键是根据正方形的边的性质和直角可通过SAS判定△BCG≌△DCE.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
10.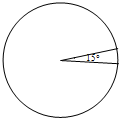 如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
 如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )| A. | 5-6箱 | B. | 6-7箱 | C. | 7-8箱 | D. | 8-9箱 |
7.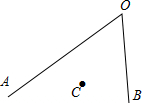 某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
 某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
14.△ABC中,AB=15,BC=14,AC=13,则△ABC的面积是( )
| A. | 96 | B. | 120 | C. | 84 | D. | 60 |
12.已知P1(-3,y1)、P2(-2,y2)是二次函数y=-2(x+1)2+1图象上的两个点,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | 无法确定 |
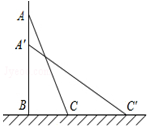 一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.