题目内容
17.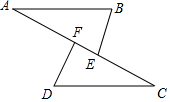 点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.条件:①②③,
结论:④(均填写序号)
证明:
分析 选择①②③得到④,组成命题为如果BE=DF,AF=CE,DF∥BE,那么∠A=∠C;利用“SAS”证明△ABE≌△CDF,然后根据相似的性质得到∠A=∠C.
解答 解:题设:①②③;
结论:④.
证明如下:∵BE∥DF,
∴∠BEA=∠DFC,
∵AF=CE,
∴AF+EF=EF+CE,
∴AE=CF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠BEA=∠DFC}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠A=∠C.
故答案为:①②③;④.
点评 本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
8.用“嘉兴”、“平安”、“创建”三个词语组句子,那么能够组成“嘉兴平安创建”或“创建平安嘉兴”的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.下列合并同类项正确的是( )
①3a+2b=5ab;②3a+b=3ab;③3a-a=3;④2R+πR=(2+π)R;
⑤7ab-7ba=0;⑥4x2y3-5x2y3=-x2y3;⑦-2-3=-5;⑧3x2+2x3=5x5.
①3a+2b=5ab;②3a+b=3ab;③3a-a=3;④2R+πR=(2+π)R;
⑤7ab-7ba=0;⑥4x2y3-5x2y3=-x2y3;⑦-2-3=-5;⑧3x2+2x3=5x5.
| A. | ①②③④ | B. | ⑤⑥⑦⑧ | C. | ⑥⑦ | D. | ④⑤⑥⑦ |
14.△ABC中,AB=15,BC=14,AC=13,则△ABC的面积是( )
| A. | 96 | B. | 120 | C. | 84 | D. | 60 |
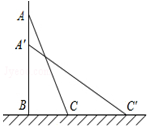 一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.