题目内容
6.不等式组$\left\{\begin{array}{l}{-x+2>0}\\{-2x<4}\end{array}\right.$的解集是-2<x<2.分析 分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出不等式组的解集.
解答 解:$\left\{\begin{array}{l}{-x+2>0①}\\{-2x<4②}\end{array}\right.$,
由①得:x<2;
由②得:x>-2,
则不等式组的解集为-2<x<2.
故答案为:-2<x<2.
点评 此题考查了解一元一次不等式组,熟练掌握不等式组取解集的方法是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.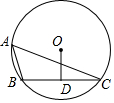 如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )
如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )
 如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )
如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
14.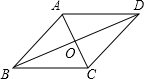 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
11.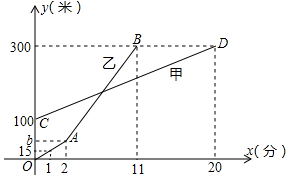 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )| A. | 165m | B. | 160m | C. | 135m | D. | 120m |
18.计算:(1)$\frac{3}{4}\sqrt{3\frac{3}{4}}×(-18\sqrt{45})$;(2)$\sqrt{2x-3y}•\sqrt{4{x}^{2}-9{y}^{2}}$.
8.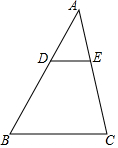 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )| A. | 4 | B. | 8 | C. | $\frac{21}{2}$ | D. | $\frac{25}{2}$ |
