题目内容
16.如图(1),将线段AB绕点A逆时针旋转2α(0°<α<90°)至AC,P是过A,B,C的三点圆上任意一点.(1)当α=30°时,如图(1),求证:PC=PA+PB;
(2)当α=45°时,如图(2),PA,PB,PC三条线段间是否还具有上述数量关系?若有,请说明理由;若不具有,请探索它们的数量关系.

分析 (1)首先在PC上截取PD=PA,易知△ABC是等边三角形,可得△PAD是等边三角形,继而可证明△ACD≌△BAP,则CD=PB,从而得出PC=PB+PA;
(2)PC=$\sqrt{2}$PA+PB,作AD⊥AP与PC交于一点D,易证△ACD≌△ABP,则CD=PB,AD=AP,根据勾股定理PD=$\sqrt{2}$PA,所以PC=$\sqrt{2}$PA+PB.
解答 证明:(1)如图(1),在PA上截取PD=PA,
∵AB=AC,∠CAB=60°,
∴△ABC为等边三角形,
∴∠APC=∠CPB=60°,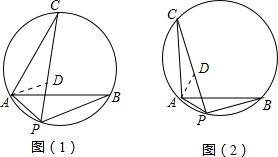
∴△APD为等边三角形,
∴AP=AD=PD,
∴∠ADC=∠APB=120°,
在△ACD和△ABP中,
$\left\{\begin{array}{l}{∠ADC=∠APB}\\{∠ACD=∠ABP}\\{AD=AP}\end{array}\right.$,
∴△ACD≌△ABP(AAS),
∴CD=PB,
∵PC=PD+DC,
∴PC=PA+PB;
(2)PC=$\sqrt{2}$PA+PB,
如图(2),作AD⊥AP与PC交于一点D,
∵∠BAC=90°,
∴∠CAD=∠BAP,
在△ACD和△ABP中,
$\left\{\begin{array}{l}{∠CAD=∠BAP}\\{AC=AB}\\{∠ACD=∠ABP}\end{array}\right.$,
∴△ACD≌△ABP,
∴CD=PB,AD=AP,
根据勾股定理PD=$\sqrt{2}$PA,
∴PC=PD+CD=$\sqrt{2}$PA+PB.
点评 此题考查了圆周角定理、等边三角形的判定与性质以及全等三角形的判定与性质.掌握辅助线的作法以及熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
7.用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第10个图案需要“O”的个数是( )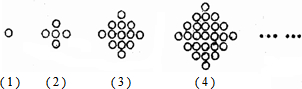

| A. | 145个 | B. | 162 | C. | 181个 | D. | 202个 |
11. 如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
 如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )| A. | 是一个定值 | B. | 有两个不同的值 | ||
| C. | 有三个不同的值 | D. | 有三个以上不同的值 |
8.下列运算正确的是( )
| A. | 32-2a2=1 | B. | a6÷a3=a2 | C. | (a-b)2=a2-b2 | D. | 2a•4a=8a2 |
5.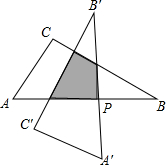 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )| A. | $\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{9}{4}$ | D. | $\frac{15}{4}$ |
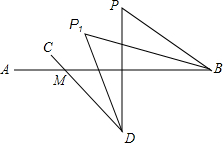 如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.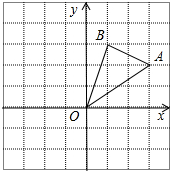 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1. 如图,将两块直角三角尺的直角顶点C叠放在一起,
如图,将两块直角三角尺的直角顶点C叠放在一起,