Question

5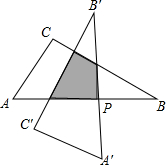．如图，在Rt△ABC中，已知：∠C=90°，∠A=60°，AC=3cm，以斜边AB的中点P为旋转中心，把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′，则旋转前后两个直角三角形重叠部分的面积为（　　）

• A． $\sqrt{3}$
• B． $\sqrt{3}$+1
• C． $\frac{9}{4}$
• D． $\frac{15}{4}$

Answer 1

分析 根据已知及勾股定理求得DP的长，再根据全等三角形的判定得到△B′PH≌△BPD，从而根据直角三角形的性质求得GH，BG的长，从而不难求得旋转前后两个直角三角形重叠部分的面积．

解答 解：如图，

在直角△DPB中，BP=AP=AC=3，
∵∠A=60°，
∴DP²+BP²=BD²，
∴x²+3²=（2x）²，
∴DP=x=$\sqrt{3}$，
∵在△B′PH和△BPD中，
$\left\{\begin{array}{l}{B′P=BP}\\{∠B′=∠B}\\{∠B′PH=∠BPD}\end{array}\right.$，
∴△B′PH≌△BPD，
∴PH=PD=$\sqrt{3}$，
∵在直角△BGH中，BH=3+$\sqrt{3}$，
∴GH=$\frac{3+\sqrt{3}}{2}$，BG=$\frac{\sqrt{3}}{2}$（3+$\sqrt{3}$），
∴S_△BGH=$\frac{1}{2}$×$\frac{3+\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$（3+$\sqrt{3}$）=$\frac{6\sqrt{3}+9}{4}$，S_△BDP=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$，
∴S_DGHP=$\frac{6\sqrt{3}+9}{4}$-$\frac{3\sqrt{3}}{2}$，
=$\frac{9}{4}$cm²．
故选：C．

点评 此题考查旋转的性质，勾股定理，三角形的全等的判定及性质，三角形的面积，综合运用知识，灵活解决问题．