题目内容
恒信专卖店专销某品牌钮扣电池,进价l2元/粒,售价20元/粒.为了促销,专卖店决定凡是一次性买10粒以上的,每多买一粒,单价就降低O.10元(例如.某人一次性买20粒,则每粒降价O.10×(20-10)=1元,就可以按19元/粒的价格购买,20粒只需380元购买),但是最低售价为16元/粒.设每一次性卖出x粒电池,商店的利润为y元.
(1)请分段写出y与x的函数关系式;
(2)有一天,一位顾客买了46粒,另一位顾客买了50粒,专卖店发现卖50粒反而比卖46粒赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低售价16元/粒至少要提高到多少?为什么?
(1)请分段写出y与x的函数关系式;
(2)有一天,一位顾客买了46粒,另一位顾客买了50粒,专卖店发现卖50粒反而比卖46粒赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低售价16元/粒至少要提高到多少?为什么?
考点:二次函数的应用
专题:
分析:(1)分0<x≤10时,lO<x≤50时,和x>50时,三种情况,表示出函数解析式即可;
(2)利用当lO<x≤50时,得出的函数解析式,探讨得出答案即可.
(2)利用当lO<x≤50时,得出的函数解析式,探讨得出答案即可.
解答:解:(1)当0<x≤10时,且x是整数时,y=(20-12)x=8x;
当lO<x≤50时,且x是整数时,y=[20-12-0.1(x-10)]x=-0.1x2+9x;
当x>50时,且x是整数时,y=(20-16)x=4x;
(2)利润y=-0.1x2+9x=-0.1(x-45)2+202.5,
由二次函数图象可,当0<x≤45时,y随x的增大而增大.
且当x=45时达到最大值,当x>45时,y随x的增大而减小.
因为需要卖的越多赚的越多,即需要y随x的增大而增大.
此时x≤45,即最低售价为20-0.1(45-10)=16.5(元).
答:最低售价16元/粒至少要提高到16.5元/粒,
当lO<x≤50时,且x是整数时,y=[20-12-0.1(x-10)]x=-0.1x2+9x;
当x>50时,且x是整数时,y=(20-16)x=4x;
(2)利润y=-0.1x2+9x=-0.1(x-45)2+202.5,
由二次函数图象可,当0<x≤45时,y随x的增大而增大.
且当x=45时达到最大值,当x>45时,y随x的增大而减小.
因为需要卖的越多赚的越多,即需要y随x的增大而增大.
此时x≤45,即最低售价为20-0.1(45-10)=16.5(元).
答:最低售价16元/粒至少要提高到16.5元/粒,
点评:此题主要考查了函数的综合应用,根据函数的对称性讨论最大值问题,需考虑自变量的取值范围.

练习册系列答案
相关题目
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )A、 |
B、 |
C、 |
D、 |

 如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;
如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;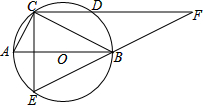 如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=
如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=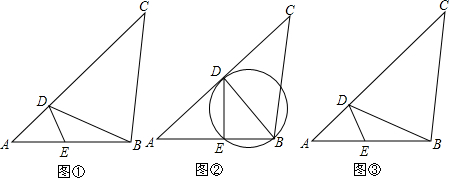
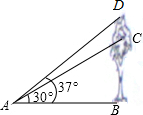 九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)
九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)