题目内容
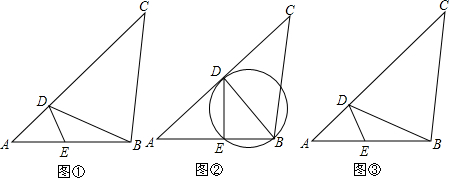
如图，△ABC是等边三角形，D为BC上的一点，∠BAD=25°，△ABD经过旋转到达△ACE的位置，那么旋转角度为（ ）| A、25° | B、45° |
| C、60° | D、30° |
考点：旋转的性质
专题：计算题
分析：根据等边三角形的性质得∠BAC=60°，AB=AC，再根据旋转的定义得到AB和AC为对应边，然后根据旋转的性质得到∠BAC等于旋转角．
解答：解：∵△ABC是等边三角形，
∴∠BAC=60°，AB=AC，
∵△ABD经过旋转到达△ACE的位置，
∴AB和AC为对应边，
∴∠BAC等于旋转角，即旋转角度为60°．
故选C．
∴∠BAC=60°，AB=AC，
∵△ABD经过旋转到达△ACE的位置，
∴AB和AC为对应边，
∴∠BAC等于旋转角，即旋转角度为60°．
故选C．
点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的性质．
练习册系列答案
相关题目
如图，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，使点B与点A重合，折痕DE，则AE的长为若二次函数f（x）=ax2+bx+c的对称轴为x=1，且其图象过点（2，0），则
的值是（ ）
| f(-1) |
| f(1) |
| A、-3 | B、-2 | C、2 | D、3 |
如图数轴上有A、B、C、D四点，根据图中各点的位置，判断哪一点所表示的数与11-2
最接近？（ ）
| 39 |
| A、A | B、B | C、C | D、D |
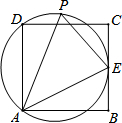如图，已知在边长为8的正方形ABCD中，E是BC边的中点，P在过A、E、D三点的圆上，则△APE面积的最大值是（ ）A、10
| ||
B、10
| ||
| C、32 | ||
D、5
|
如图所示的几何体的主视图是（ ）A、 |
B、 |
C、 |
D、 |
