题目内容
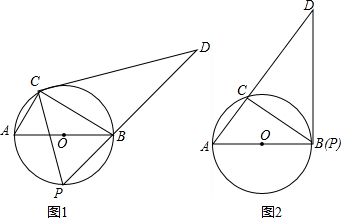
7.如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧AB向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.(1)求证:△ABC∽△PDC;
(2)如图2,当点P到达B点时,求CD的长;
(3)设CD的长为x.在点P的运动过程中,x的取值范围为2$\sqrt{3}$≤x≤4$\sqrt{3}$(请直接写出答案).
分析 (1)根据两角对应相等的三角形相似即可证明;
(2)由△ABC∽△PDC,可得∠D=∠ABC=30°,由此即可解决问题;
(3)由△ABC∽△PDC.可得$\frac{PC}{DC}$=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,推出CD=$\sqrt{3}$PC,由PC的最小值为2,最大值为直径4,即可推出CD的最小值为2$\sqrt{3}$,CD的最大值为4$\sqrt{3}$;
解答 (1)证明:如图1中,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠PCD,
又∵∠A=∠P,
∴△ABC∽△PDC.
(2)解:如图2中,
∵∠ABC=30°,AB=4,
∴BC=$2\sqrt{3}$,
∵△ABC∽△PDC,
∴∠D=∠ABC=30°,
∴CD=6.
(3)∵△ABC∽△PDC.
∴$\frac{PC}{DC}$=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∴CD=$\sqrt{3}$PC,
∵PC的最小值为2,最大值为直径4,
∴CD的最小值为2$\sqrt{3}$,CD的最大值为4$\sqrt{3}$,
∴2$\sqrt{3}$≤x≤4$\sqrt{3}$,
故答案为2$\sqrt{3}$≤x≤4$\sqrt{3}$.
点评 本题考查圆综合题、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形的条件解决问题,学会利用圆中是最长的弦解决最值问题,属于中考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
15.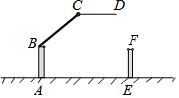 一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
 一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )| A. | 180° | B. | 270° | C. | 300° | D. | 360° |
12.关于x的方程ax2-2x+1=0有两个实数根,则a的取值范围是( )
| A. | .a≤1 | B. | .a<1 | C. | .a≤1且a≠0 | D. | a<1且a≠0 |

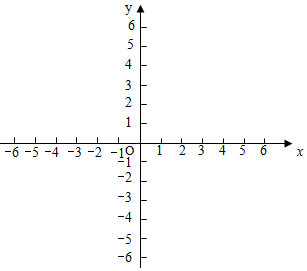 已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).