题目内容
12.某年,埃博拉病毒在非洲肆虐,某制药厂研制出一种提高免疫力的药品,为赶制这批紧销药品投放市场,立即组织100名工人进行生产,已知生产这种药品有两道工序:一是由原材料生产半产品,二是由半产品生产出药品.由于半产品不易保存,剩余半成品当天必须卖给附近大厂,每名工人每天可生产半成品30千克或由半成品生产药品4千克(两项选一项),每2千克半成品只能生产1千克药品.若药品出厂价为30元/千克,半成品价格为3元/千克.(1)设厂长每天安排x名工人生产半成品,销售药品收入y1元,请用x的代数式表示销售药品收入y1;设当天剩余半成品全部卖出收入为y2元,请用x的代数式表示y2,并求出这个问题中x的取值范围.
(2)为了使每天收益最大,请你帮厂长策划:每天安排多少名工人生产半产品?并求出这个最大收益.
分析 (1)根据题意构建一次函数y1、y2,构建不等式求出自变量的取值范围即可;
(2)设每天的收入为w元,则有w=y1+y2=-120x+12000+114x-2400=-6x+9600,因为k=-6<0,所以w随x的增大而减小,推出x=22时,w有最小值,由此即可解决问题;
解答 解:(1)y1=(100-x)×4×30=-120x+12000,
y2=[30x-(100-x)×4×2]×3=114x-2400,
∵$\left\{\begin{array}{l}{12000-120x≥0}\\{114x-2400≥0}\\{x为整数}\end{array}\right.$,
∴$\frac{400}{19}$≤x≤100且x为整数.
(2)设每天的收入为w元,
w=y1+y2=-120x+12000+114x-2400=-6x+9600,
∵k=-6<0,
w随x的增大而减小,
∴x=22时,w有最小值,最小值为9468元.
点评 本题考查一次函数的应用,不等式组等整数,解题的关键是理解题意,学会利用函数的性质解决最值值问题,属于中考常考题型.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
4.若|a|<2,且a是整数,那么a为( )
| A. | 2,1,0 | B. | -2,-1,0,1,2 | C. | -1,0,1 | D. | 0,-1,-2 |
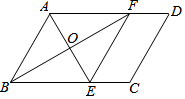 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF. 如图,已知AD=AE,∠BEC=∠CDB,BD、CE相交于点O.
如图,已知AD=AE,∠BEC=∠CDB,BD、CE相交于点O.
 如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.