题目内容
15.在平面直角坐标系xOy中,对于双曲线y=$\frac{m}{x}$(m>0)和双曲线y=$\frac{n}{x}$(n>0),如果m=2n,则称双曲线y=$\frac{m}{x}$(m>0)和双曲线y=$\frac{n}{x}$(n>0)为“倍半双曲线”,双曲线y=$\frac{m}{x}$(m>0)是双曲线y=$\frac{n}{x}$(n>0)的“倍双曲线”,双曲线y=$\frac{n}{x}$(n>0)是双曲线y=$\frac{m}{x}$(m>0)的“半双曲线”,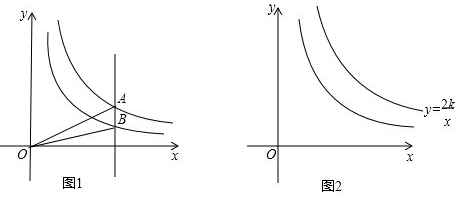
(1)请你写出双曲线y=$\frac{3}{x}$的“倍双曲线”是y=$\frac{6}{x}$;双曲线y=$\frac{8}{x}$的“半双曲线”是y=$\frac{4}{x}$;
(2)如图1,在平面直角坐标系xOy中,已知点A是双曲线y=$\frac{4}{x}$在第一象限内任意一点,过点A与y轴平行的直线交双曲线y=$\frac{4}{x}$的“半双曲线”于点B,求△AOB的面积;
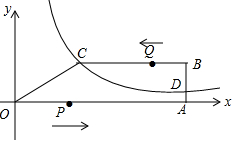
(3)如图2,已知点M是双曲线y=$\frac{2k}{x}$(k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y=$\frac{2k}{x}$的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y=$\frac{2k}{x}$的“半双曲线”于点P,若△MNP的面积记为S△MNP,且1≤S△MNP≤2,求k的取值范围.
分析 (1)直接利用“倍双曲线”的定义即可;
(2)利用双曲线的性质即可;
(3)先利用双曲线上的点设出M的横坐标,进而表示出M,N的坐标;
方法一、用三角形的面积公式建立不等式即可得出结论;
方法二、利用相似三角形的性质得出△PMN的面积,进而建立不等式即可得出结论.
解答 解:(1)由“倍双曲线”的定义
∴双曲线y=$\frac{3}{x}$,的“倍双曲线”是y=$\frac{6}{x}$;
双曲线y=$\frac{8}{x}$ 的“半双曲线”是y=$\frac{4}{x}$.
故答案为y=$\frac{6}{x}$,y=$\frac{4}{x}$;
(2)如图1,
∵双曲线y=$\frac{4}{x}$的“半双曲线”是y=$\frac{2}{x}$,
∴△AOD的面积为2,△BOD的面积为1,
∴△AOB的面积为1.
(3)解法一:如图2,
依题意可知双曲线$y=\frac{2k}{x}(k>0)$的“半双曲线”为$y=\frac{k}{x}(k>0)$,
设点M的横坐标为m,则点M坐标为(m,$\frac{2k}{m}$),点N坐标为(m,$\frac{k}{m}$),
∴CM=$\frac{2k}{m}$,CN=$\frac{k}{m}$.
∴MN=$\frac{2k}{m}$-$\frac{k}{m}$=$\frac{k}{m}$.
同理PM=m-$\frac{m}{2}$=$\frac{m}{2}$.
∴S△PMN=$\frac{1}{2}$MN•PM=$\frac{k}{4}$
∵1≤S△PMN≤2,
∴1≤$\frac{k}{4}$≤2.
∴4≤k≤8,
解法二:如图3,
依题意可知双曲线$y=\frac{2k}{x}(k>0)$的“半双曲线”为$y=\frac{k}{x}(k>0)$,
设点M的横坐标为m,则点M坐标为(m,$\frac{2k}{m}$),点N坐标为(m,$\frac{k}{m}$),
∴点N为MC的中点,同理点P为MD的中点.
连接OM,
∵$\frac{PM}{OC}=\frac{MN}{MC}=\frac{1}{2}$,
∴△PMN∽△OCM.
∴$\frac{{S}_{△PMN}}{{S}_{△OCM}}=\frac{1}{4}$.
∵S△OCM=k,
∴S△PMN=$\frac{k}{4}$.
∵1≤S△PMN≤2,
∴1≤$\frac{k}{4}$≤2.
∴4≤k≤8.
点评 此题是反比例函数综合题,主要考查了新定义,双曲线的性质,三角形的面积公式,相似三角形的判定和性质,解(1)的关键是理解新定义,解(2)的关键是三角形的面积公式的应用,解(3)的关键是建立不等式求解.

 如图,在直角坐标系中,O是原点,点C的坐标为C(12,5),点A在x轴的正半轴上,四边形OABC是直角梯形,经过点C的反比例函数的图象交AB于点D,且点D的纵坐标为2.
如图,在直角坐标系中,O是原点,点C的坐标为C(12,5),点A在x轴的正半轴上,四边形OABC是直角梯形,经过点C的反比例函数的图象交AB于点D,且点D的纵坐标为2.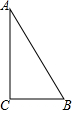 如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
 运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a)
运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a)