题目内容
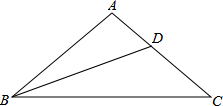 问题:在△ABC中,AB=AC,∠A=100°,BD为∠B的平分线,探究AD、BD、BC之间的数量关系.
问题:在△ABC中,AB=AC,∠A=100°,BD为∠B的平分线,探究AD、BD、BC之间的数量关系.请你完成下列探究过程:
(1)观察图形,猜想AD、BD、BC之间的数量关系为
(2)在对(1)中的猜想进行证明时,当推出∠ABC=∠C=40°后,可进一步推出∠ABD=∠DBC=
(3)为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在BC上截取BE=BD,连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)AD+BD=BC;
(2)由等腰三角形的性质及角平分线的性质可得∠ABD=∠DBC=20°;
(3)在BC上截取BF=BA,连接DF,在BC上截取BE=BD,连接DE,先证得△ABD≌△FBD,∠DFB=∠A=100°,∠DFC=80°,再得∠BED=∠BDE=80°,所以∠DFE=∠FED.再推得∠EDC=∠C,DE=EC,AD=EC,于是AD+BD=BC.
(2)由等腰三角形的性质及角平分线的性质可得∠ABD=∠DBC=20°;
(3)在BC上截取BF=BA,连接DF,在BC上截取BE=BD,连接DE,先证得△ABD≌△FBD,∠DFB=∠A=100°,∠DFC=80°,再得∠BED=∠BDE=80°,所以∠DFE=∠FED.再推得∠EDC=∠C,DE=EC,AD=EC,于是AD+BD=BC.
解答:解:(1)AD+BD=BC;
(2)∵AB=AC,∠A=100°
∴∠ABC=∠C=40°
∵BD为∠B的平分线,
∴∠ABD=∠DBC=20°;
(3)在BC上截取BF=BA,连接DF,在BC上截取BE=BD,连接DE,

∵BD为∠B的平分线,
∴∠ABD=∠DBC.
∴在△ABD和△FBD中,
,
∴△ABD≌△FBD.
∵∠A=100°,
∴∠DFB=∠A=100°,
∴∠DFC=80°,
∵BE=BD,∠DBC=20°,
∴∠BED=∠BDE=80°,∠DFE=∠FED.
∴DF=DE.
∵∠FED=80°,∠C=40°,
∴∠EDC=40°.
∴∠EDC=∠C.
∴DE=EC.
∴AD=EC.
∴AD+BD=BC.
(2)∵AB=AC,∠A=100°
∴∠ABC=∠C=40°
∵BD为∠B的平分线,
∴∠ABD=∠DBC=20°;
(3)在BC上截取BF=BA,连接DF,在BC上截取BE=BD,连接DE,

∵BD为∠B的平分线,
∴∠ABD=∠DBC.
∴在△ABD和△FBD中,
|
∴△ABD≌△FBD.
∵∠A=100°,
∴∠DFB=∠A=100°,
∴∠DFC=80°,
∵BE=BD,∠DBC=20°,
∴∠BED=∠BDE=80°,∠DFE=∠FED.
∴DF=DE.
∵∠FED=80°,∠C=40°,
∴∠EDC=40°.
∴∠EDC=∠C.
∴DE=EC.
∴AD=EC.
∴AD+BD=BC.
点评:本题主要考查了全等三角形的判定与性质以及等腰三角形的性质.正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程2x2+3x-4的根的情况是( )
| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、有两个实数根 |
 李明乘车从永康到某景区旅游,同时王红从该景区返回永康.线段OB表示李明离永康的路程S1(km)与时间t(h)的函数关系;线段AC表示王红离永康的路程S2(km)与时间t(h)的函数关系.行驶1小时,李明、王红离永康的路程分别为100km、280km,王红从景区返回永康用了4.5小时.(假设两人所乘的车在同一线路上行驶)
李明乘车从永康到某景区旅游,同时王红从该景区返回永康.线段OB表示李明离永康的路程S1(km)与时间t(h)的函数关系;线段AC表示王红离永康的路程S2(km)与时间t(h)的函数关系.行驶1小时,李明、王红离永康的路程分别为100km、280km,王红从景区返回永康用了4.5小时.(假设两人所乘的车在同一线路上行驶)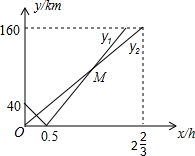 某次海军舰艇演习中,甲、乙两舰艇同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束.已知B港位于A港、C岛之间,且A、B、C在一条直线上.设甲、乙两舰艇行驶x(h)后,与B港的距离分别为y1和y2(km),y1、y2与x的函数关系如图所示.
某次海军舰艇演习中,甲、乙两舰艇同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束.已知B港位于A港、C岛之间,且A、B、C在一条直线上.设甲、乙两舰艇行驶x(h)后,与B港的距离分别为y1和y2(km),y1、y2与x的函数关系如图所示. 如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°.
如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°. 如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA. 如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.
如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.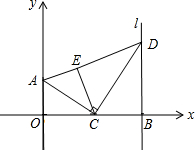 如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)
如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)