题目内容

如图，矩形ABCD中，BC=8，对角线BD=10，求tan∠ACB．
考点：矩形的性质,勾股定理
专题：
分析：首先根据矩形对角线相等可得AC=BD=10，再根据勾股定理计算出AB长，再根据三角函数的定义可得答案．
解答：解：∵四边形ABCD是矩形，
∴AC=BD=10，
在Rt△ABC中，
AB=
AC2-BC2
=
102-82
=6，
∴tan∠ACB=
AB
BC
=
6
8
=
3
4
．
点评：此题主要考查了勾股定理、矩形的性质，关键是掌握矩形对角线相等．
练习册系列答案
相关题目
下列各图形都是由同样大小的菱形按一定规律组成的，其中第（1）个图形中菱形的个数是1，第（2）个图形中菱形的个数是5，第（3）个图形中菱形的个数是14，第（4）个图形中菱形的个数是30，…，则第（8）个图形中菱形的个数是（　　）
A、196B、204
C、214D、228
“低碳生活，绿色出行”，自行车正逐渐成为人们喜爱的交通工具．某运动商城的自行车销售量自2013年起逐月增加，据统计，该商城1月份销售自行车64辆，3月份销售了100辆．若该商城前2、3月份自行车销量的月平均增长率相同，求该商城2、3月份的月平均增长率．
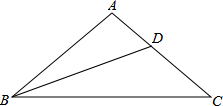问题：在△ABC中，AB=AC，∠A=100°，BD为∠B的平分线，探究AD、BD、BC之间的数量关系．
请你完成下列探究过程：
（1）观察图形，猜想AD、BD、BC之间的数量关系为
 
．
（2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC=
 
度．
（3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE，在此基础上继续推理可使问题得到解决．你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明．也可以选用其它的方法证明你的猜想．
如图，抛物线y=ax2-5ax+4a与x轴相交于点A、B，且过点C（5，4）．
（1）求a的值和该抛物线顶点P的坐标；
（2）求三角形ABC的面积；
（3）将抛物线先向左平移2个单位，再向上平移3个单位，写出平移后抛物线的解析式．
在不透明的布袋中装有1个白球，2个红球，它们除颜色外其余完全相同．
（1）从袋中任意摸出两个球，试用树状图或表格列出所有等可能的结果，并求摸出的球恰好是两个红球的概率；
（2）若在布袋中再添加x个白球，充分搅匀，从中摸出一个球，使摸到白球的概率为
3
5
，求添加的白球个数x．
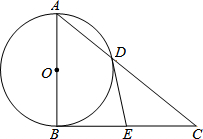如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE．
（1）求证：DE与⊙O相切．
（2）若tanC=
5
2
，DE=2，求AD的长．
已知：关于x的一元二次方程（m-1）x2-2mx+m+1=0 （m＞1）．
（1）求证：方程总有两个不相等的实数根．
（2）m为何整数时，此方程的两个实数根都为正整数？
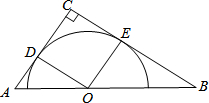如图，在△ABC中，∠C=90°，点O在斜边AB上，以O为圆心的⊙O分别与AC，BC相切于点D，E，连接OD，OE．
（1）求证：四边形CDOE是正方形；
（2）当AC=4，BC=6时，求⊙O的半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网