��Ŀ����
 ��ͼ����A�������ǣ�0��2������B��x���������ϵĵ㣬����B��ֱ��l��ֱ��x�ᣬ��CΪ�߶�OB�ϵĶ��㣬����AC������C��CD��AC��ֱ��l�ڵ�D������BCD��CD��������ECD��λ�ã�����AE�����B�������ǣ�m��0������C�������ǣ�n��0��
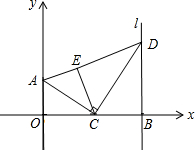
��ͼ����A�������ǣ�0��2������B��x���������ϵĵ㣬����B��ֱ��l��ֱ��x�ᣬ��CΪ�߶�OB�ϵĶ��㣬����AC������C��CD��AC��ֱ��l�ڵ�D������BCD��CD��������ECD��λ�ã�����AE�����B�������ǣ�m��0������C�������ǣ�n��0����1���ú�m��n�Ĵ���ʽ��ʾ��D�����ꣻ
��2������A��E��D������ͬһֱ����ʱ����m��n֮���������ϵ��
��3�����ڵ�C���˶���������Ψһλ��ʹ��AE��x�ᣬ��m��ֵ��
���㣺�������ۺ���
ר�⣺
��������1��������֪���������ACO+��BCD=90�㣬��ACO+��OAC=90�㣬�ó���BCD=��OAC���ٸ���AA�ó���AOC�ס�CBD���ó�
=
�����DB=
n��m-n��=-
n2+
mn�����ɵó�D�����ꣻ
��2�����ݡ�BCD��CD��������ECD��λ�ã��ó���DEC=��DBC=90�㣬����A��E��D������ͬһֱ����ʱ���ó���AOC=��AEC���ٸ��ݡ�BCD=��ECD���ó���ACO=��ACE���ٸ���AAS�ó���AOC�ա�AEC���ó�OC=EC=BC���Ӷ��ó�m��n֮���������ϵ��
��3����AE��x��ʱ���ó���EAC=��ACE��EA=EC=CB=m-n����EF��OC���þ���AOFE�����ݾ��ε��ص�ó�CF=|n-��m-n��|=|2n-m|���ٸ��ݹ��ɶ����ó�EF2+FC2=EC2��Ȼ����������ó�3n2-2mn+4=0���ٸ��ݵ�C���˶���������Ψһλ��ʹ��AE��x�ᣬ�ó���=��2m��2-4��3��4=0���������������m��ֵ���ɣ�
| CB |
| AO |
| DB |
| OC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��2�����ݡ�BCD��CD��������ECD��λ�ã��ó���DEC=��DBC=90�㣬����A��E��D������ͬһֱ����ʱ���ó���AOC=��AEC���ٸ��ݡ�BCD=��ECD���ó���ACO=��ACE���ٸ���AAS�ó���AOC�ա�AEC���ó�OC=EC=BC���Ӷ��ó�m��n֮���������ϵ��
��3����AE��x��ʱ���ó���EAC=��ACE��EA=EC=CB=m-n����EF��OC���þ���AOFE�����ݾ��ε��ص�ó�CF=|n-��m-n��|=|2n-m|���ٸ��ݹ��ɶ����ó�EF2+FC2=EC2��Ȼ����������ó�3n2-2mn+4=0���ٸ��ݵ�C���˶���������Ψһλ��ʹ��AE��x�ᣬ�ó���=��2m��2-4��3��4=0���������������m��ֵ���ɣ�
����⣺��1����CD��AC��DB��BO��AO��BO��
���AOC=��CBD=90�㣬��ACD=90�㣬
���ACO+��BCD=90�㣬��ACO+��OAC=90�㣬
���BCD=��OAC��
���AOC�ס�CBD��
��
=
����
=
��
��DB=
n��m-n��=-
n2+
mn��
��D��m��-
n2+
mn����
��2���ߡ�BCD��CD��������ECD��λ�ã�
���DEC=��DBC=90�㣬
����A��E��D������ͬһֱ����ʱ����AEC=180��-��DEC=90�㣬
���AOC=��AEC��
�ߡ�ACO+��BCD=90�㣬��ACE+��ECD=90��
�֡ߡ�BCD=��ECD��
���ACO=��ACE��
�ڡ�AOC���AEC�У�
��
���AOC�ա�AEC��AAS����
��OC=EC=BC����n=m-n��
��m=2n��
��3����AE��x��ʱ����EAC=��ACO����ACO=��ACE��
���EAC=��ACE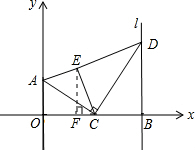
��EA=EC=CB=m-n��
��EF��OC���þ���AOFE��
��EF=AO=2��OF=AE=m-n��
��CF=|n-��m-n��|=|2n-m|��
Rt��FCE�У����ݹ��ɶ�����EF2+FC2=EC2��
��22+��2n-m��2=��m-n��2��
������3n2-2mn+4=0��
�ߵ�C���˶���������Ψһλ��ʹ��AE��x�ᣬ
���=��2m��2-4��3��4=0��m=��2
����ֵ��ȥ����
��m=2
��
���AOC=��CBD=90�㣬��ACD=90�㣬
���ACO+��BCD=90�㣬��ACO+��OAC=90�㣬
���BCD=��OAC��
���AOC�ס�CBD��
��
| CB |
| AO |
| DB |
| OC |
| m-n |
| 2 |
| DB |
| n |
��DB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��D��m��-
| 1 |
| 2 |
| 1 |
| 2 |
��2���ߡ�BCD��CD��������ECD��λ�ã�
���DEC=��DBC=90�㣬
����A��E��D������ͬһֱ����ʱ����AEC=180��-��DEC=90�㣬
���AOC=��AEC��
�ߡ�ACO+��BCD=90�㣬��ACE+��ECD=90��
�֡ߡ�BCD=��ECD��
���ACO=��ACE��
�ڡ�AOC���AEC�У�
|
���AOC�ա�AEC��AAS����
��OC=EC=BC����n=m-n��
��m=2n��
��3����AE��x��ʱ����EAC=��ACO����ACO=��ACE��
���EAC=��ACE

��EA=EC=CB=m-n��
��EF��OC���þ���AOFE��
��EF=AO=2��OF=AE=m-n��
��CF=|n-��m-n��|=|2n-m|��
Rt��FCE�У����ݹ��ɶ�����EF2+FC2=EC2��
��22+��2n-m��2=��m-n��2��
������3n2-2mn+4=0��
�ߵ�C���˶���������Ψһλ��ʹ��AE��x�ᣬ
���=��2m��2-4��3��4=0��m=��2
| 3 |
��m=2
| 3 |
���������⿼���������ε��ۺϣ��õ���֪ʶ�������������κ�ȫ�������ε��ж������ʡ����ɶ����ȣ��ؼ��Ǹ������⻭�������ߣ��ó�CF��ֵ��

��ϰ��ϵ�д�
�����Ŀ
�߳�Ϊ4�ĵȱ������������ĸ����ڵ�ֱ����ת180�㣬���õ�Բ�ı����Ϊ��������
| A��12�� | ||
B����4
| ||
C����8
| ||
| D��8�� |
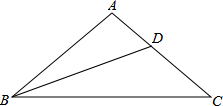 ���⣺�ڡ�ABC�У�AB=AC����A=100�㣬BDΪ��B��ƽ���ߣ�̽��AD��BD��BC֮���������ϵ��
���⣺�ڡ�ABC�У�AB=AC����A=100�㣬BDΪ��B��ƽ���ߣ�̽��AD��BD��BC֮���������ϵ��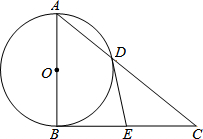 ��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC�ߵ��е㣬����DE��
��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC�ߵ��е㣬����DE�� ��ͼ����֪AC��BC��BD��AD��AC��BD����O��AC=BD����֤��
��ͼ����֪AC��BC��BD��AD��AC��BD����O��AC=BD����֤��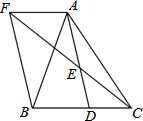 ��ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BF��ƽ���ߣ���CE���ӳ����ڵ�F����AF=BD������BF�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�
��ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BF��ƽ���ߣ���CE���ӳ����ڵ�F����AF=BD������BF�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�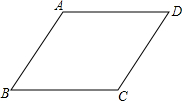 ��ͼ��������ABCD�У�AB=a����ABC=����������ABCD�Ƶ�B˳ʱ����ת����ת��С��90�㣩����A��C��D�ֱ�����A�䡢C�䡢D�䴦����A��C���BCʱA��D=
��ͼ��������ABCD�У�AB=a����ABC=����������ABCD�Ƶ�B˳ʱ����ת����ת��С��90�㣩����A��C��D�ֱ�����A�䡢C�䡢D�䴦����A��C���BCʱA��D=