题目内容
已知a，b，c是△ABC的三边，下列条件：（1）∠A+∠B=∠C；（2）a2=（c+b）（c-b）；（3）a=4，b=5，c=6，能判定△ABC是直角三角形的有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：勾股定理的逆定理,三角形内角和定理
专题：
分析：根据三角形内角和定理可判定（1）；由勾股定理的逆定理可判定（2）、（3）；可得到答案．
解答：解：（1）当∠A+∠B=∠C时，结合∠A+∠B+∠C=180°可求得∠C=90°，所以△ABC是直角三角形，所以（1）能判定；
（2）当a2=（c+b）（c-b）时，整理可得a2=c2-b2，即a2+b2=c2，满足勾股定理的逆定型，所以（2）能判定△ABC是直角三角形；
（3）当a=4，b=5，c=6时，a2+b2=16+25=41≠62，即a2+b2≠c2，所以（3）不能；
综上可知能判定△ABC为直角三角形的有两个．
故选C．
（2）当a2=（c+b）（c-b）时，整理可得a2=c2-b2，即a2+b2=c2，满足勾股定理的逆定型，所以（2）能判定△ABC是直角三角形；
（3）当a=4，b=5，c=6时，a2+b2=16+25=41≠62，即a2+b2≠c2，所以（3）不能；
综上可知能判定△ABC为直角三角形的有两个．
故选C．
点评：本题主要考查直角三角形的判定，掌握直角三角形的判定方法是解题的关键，即①勾股定理的逆定理，②直角三角形的定义．
练习册系列答案
相关题目
下列调查中需要做普查的是（ ）
| A、了解一批炮弹的命中精度 |
| B、调查全国中学生的上网情况 |
| C、审查某文章中的错别字 |
| D、考查某种农作物的长势 |
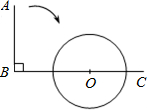如图，∠ABC=90°，O为射线BC上一点，以点O为圆心，
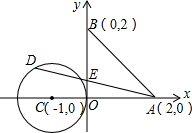如图，已知A，B两点的坐标分别为（2，0），（0，2），⊙C的圆心坐标为（-1，0），半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是多少？（写解题过程）
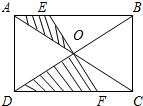如图，已知长方形ABCD的边长分别为7和4，对角线AC、BD交于点O，EF过点O分别交AB、CD于点E、F，则图中阴影部分的面积为（ ）
某种蓄电池的电压为定值，使用此电源时，电流I（A）与可变电阻R（Ω）之间的函数关系如图所示，当用电器的电流为12A时，用电器的可变电阻为