题目内容
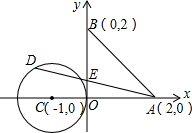 如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是多少?(写解题过程)
如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是多少?(写解题过程)考点:切线的性质,一次函数图象上点的坐标特征
专题:
分析:由于OA的长为定值,若△ABE的面积最小,则BE的长最短,此时AD与⊙相切;可连接CD,在Rt△ADC中,由勾股定理求得AD的长,易证得△AEO∽△ACD,根据相似三角形的对应边成比例,可求出BE的值,进而可根据三角形的面积公式得解.
解答: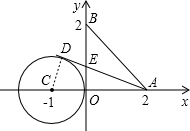 解:若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
解:若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
Rt△ACD中,CD=1,AC=OC+OA=3;
由勾股定理,得:AD=2
;
∵∠ADC=∠AOE=90°,∠CAD=∠EAO,
∴△ACD∽△AEO,
∴
=
,
∴OE=
,
∴BE=2-
,
∴S△ABE=
×2×(2-
)=2-
;
 解:若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
解:若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;Rt△ACD中,CD=1,AC=OC+OA=3;
由勾股定理,得:AD=2
| 2 |
∵∠ADC=∠AOE=90°,∠CAD=∠EAO,
∴△ACD∽△AEO,
∴
| OE |
| CD |
| OA |
| AD |
∴OE=
| ||
| 2 |
∴BE=2-
| ||
| 2 |
∴S△ABE=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:此题主要考查了切线的性质、相似三角形的性质、三角形面积的求法等知识;能够正确的判断出△BE面积最小时AD与⊙C的位置关系是解答此题的关键.

练习册系列答案
相关题目
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=67°,那么∠2的度数是( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=67°,那么∠2的度数是( )| A、67° | B、33° |
| C、20° | D、23° |
 如图,让圆形转盘自由转动一次,指针落在白色区域的概率是( )
如图,让圆形转盘自由转动一次,指针落在白色区域的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在平面直角坐标系中,点P(-2,3)关于y轴的对称点的坐标为( )
| A、(2,-3) |
| B、(2,3) |
| C、(-2,-3) |
| D、(-2,3) |

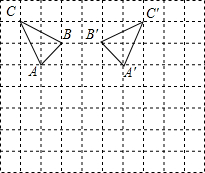 在如图所示的网格(每个小正方形的边长为1)中,△ABC的顶点A的坐标为(-2,1).
在如图所示的网格(每个小正方形的边长为1)中,△ABC的顶点A的坐标为(-2,1).