题目内容
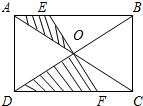如图，已知长方形ABCD的边长分别为7和4，对角线AC、BD交于点O，EF过点O分别交AB、CD于点E、F，则图中阴影部分的面积为（ ）| A、5 | B、6 | C、7 | D、8 |
考点：矩形的性质
专题：
分析：图中阴影部分的面积是△DCO的面积，则利用矩形的性质可以求得AB边上的高线为
AD，依据三角形的面积公式进行解答即可．
| 1 |
| 2 |
解答：解：如图，∵四边形ABCD是矩形，
∴AB=DC，AB∥DC，且OA=OC，
∴△AEO∽△CFO，
∴AE：CF=OA：OC=1：1，
∴S△AEO：S△CFO=1：1，
即S△AEO=S△CFO，
∴S阴影=S△AEO+S△DFO=S△CFO+S△DFO=S△DCO，即S阴影=
CD×
AD=
×7×
×4=7．
故选：C．
解：如图，∵四边形ABCD是矩形，∴AB=DC，AB∥DC，且OA=OC，
∴△AEO∽△CFO，
∴AE：CF=OA：OC=1：1，
∴S△AEO：S△CFO=1：1，
即S△AEO=S△CFO，
∴S阴影=S△AEO+S△DFO=S△CFO+S△DFO=S△DCO，即S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选：C．
点评：本题考查了矩形性质，相似三角形的性质和判定的应用，关键是求出阴影部分的面积等于△DCO的面积．
练习册系列答案
相关题目
已知线段AB两端的坐标A（4，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的
后得到线段CD，A点的对应点为C点，则端点C的坐标为（ ）
| 1 |
| 2 |
| A、（2，3） |
| B、（2，1） |
| C、（4，3） |
| D、（4，1） |
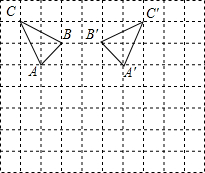在如图所示的网格（每个小正方形的边长为1）中，△ABC的顶点A的坐标为（-2，1）．
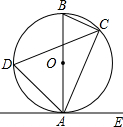如图，已知AB是⊙O的直径，点C、D在⊙O的上，点E在⊙O的外，∠EAC=∠D=60°．