题目内容
6.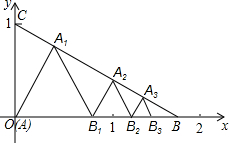 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{n}}$ | B. | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C. | $\frac{3}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n-1}}$ |
分析 根据题目已知条件可推出,AA1=$\frac{\sqrt{3}}{2}$OC=$\frac{\sqrt{3}}{2}$,B1A2=$\frac{1}{2}$A1B1=$\frac{\sqrt{3}}{{2}^{2}}$,依此类推,可求得第n个等边三角形的边长.
解答 解:∵OB=$\sqrt{3}$,OC=1,
∴BC=2,
∴∠OBC=30°,∠OCB=60°.
∵△AA1B1为等边三角形,∠A1AB1=60°,
∴∠COA1=30°,
∴∠CA1O=90°.
在Rt△CAA1中,AA1=$\frac{\sqrt{3}}{2}$OC=$\frac{\sqrt{3}}{2}$,
同理得:B1A2=$\frac{1}{2}$A1B1=$\frac{\sqrt{3}}{{2}^{2}}$,
依此类推,第n个等边三角形的边长等于$\frac{\sqrt{3}}{{2}^{2}}$,
故选A.
点评 本题主要考查一次函数图象上的点的坐标特征,等边三角形的性质及解直角三角形,解题的关键是通过计算,发现边长的规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列各图中,可以由一个正方形的平面展开图得到的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列各图经过折叠能围成直棱柱的是( )
| A. | 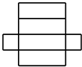 | B. |  | C. | 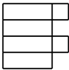 | D. |  |
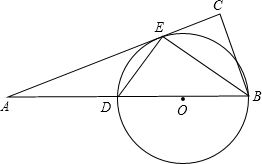 如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE
如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1.则弧BD的长是$\frac{2\sqrt{3}π}{9}$.
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1.则弧BD的长是$\frac{2\sqrt{3}π}{9}$.