题目内容
18.先化简$\frac{{x}^{2}-1}{{x}^{2}+x}$÷(x-$\frac{2x-1}{x}$),其中x满足x2-5x-6=0.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x-1}{x}$÷$\frac{(x-1)^{2}}{x}$
=$\frac{x-1}{x}$•$\frac{x}{(x-1)^{2}}$
=$\frac{1}{x-1}$,
∵x满足x2-5x-6=0,即(x-6)(x+1)=0,
∴x1=6,x2=-1,
∴当x=6时,原式=$\frac{1}{6-1}$=$\frac{1}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.已知y=$\sqrt{2x-5}$+$\sqrt{5-2x}$-3,则2xy的值为( )
| A. | $\frac{15}{2}$ | B. | 15 | C. | -$\frac{15}{2}$ | D. | -15 |
6.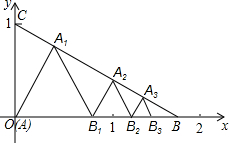 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{n}}$ | B. | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C. | $\frac{3}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n-1}}$ |
13. 一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )
一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )
 一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )
一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )| A. | 和 | B. | 谐 | C. | 泰 | D. | 州 |
3.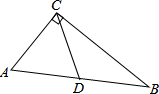 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
8.下列计算正确的是( )
| A. | -(-a)4÷a2=-a2 | B. | (2a+3b)(2a-3b)=2a2-3b2 | ||
| C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy2 | D. | 3ab-2ab=1 |
 如图,在△ABC中,∠ABC=50°,∠ACB=70°,延长CB至D,使BD=BA,延长BC至E,使CE=CA,则∠DAE=120°.
如图,在△ABC中,∠ABC=50°,∠ACB=70°,延长CB至D,使BD=BA,延长BC至E,使CE=CA,则∠DAE=120°.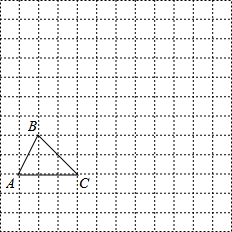 如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).