题目内容
1.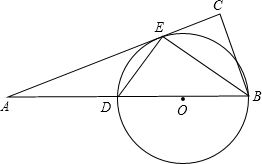 如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE
如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,AE=4$\sqrt{2}$.求DE的长.
分析 (1)连接OE,则OB=OE,即可得出∠OBE=∠OEB,再由已知得出∠OEB=∠CBE,则OE∥BC,从而证出OE⊥AC;
(2)通过相似三角形△ADE∽△AEB的对应边成比例来求DE的长度.
解答 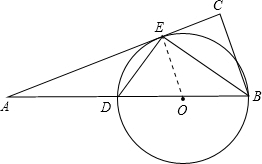 解:(1)连接OE.
解:(1)连接OE.
∴OB=OE,
∴∠OBE=∠OEB,
∵∠CBE=∠DBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∵BC⊥AE,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)由(1)知,OE⊥AC.
在直角△AEO中,AE=4$\sqrt{2}$,OE=2,AO=AD+2,则由勾股定理得到:AE2+OE2=AO2,即32+4=(AD+2)2,
解得 AD=4(舍去负值).
则AB=AD+4=10,AO=AD+2=8.
∵OE∥BC,
∴$\frac{AO}{AB}$=$\frac{OE}{BC}$=$\frac{AE}{AC}$,即$\frac{8}{10}$=$\frac{2}{BC}$=$\frac{4\sqrt{2}}{4\sqrt{2}+EC}$,则BC=$\frac{5}{2}$,EC=$\sqrt{2}$.
∴在直角△BCE中,由勾股定理得到:BE=$\sqrt{E{C}^{2}+B{C}^{2}}$=$\sqrt{2+\frac{25}{4}}$=$\frac{\sqrt{33}}{2}$.
又∵∠A=∠A,∠AED=∠ABE,
∴△ADE∽△AEB,
∴$\frac{AE}{AB}$=$\frac{DE}{BE}$,即$\frac{4\sqrt{2}}{10}$=$\frac{DE}{\frac{\sqrt{33}}{2}}$,
解得 DE=$\frac{\sqrt{66}}{5}$.
点评 本题考查了切线的性质和判定,勾股定理以及圆周角定理,是基础知识要熟练掌握.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

| A. | 射线有一个端点 | B. | 线段有两个端点 | ||
| C. | 两点确定一条直线 | D. | 两点之间,直线最短 |
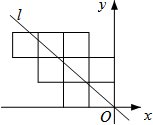 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )| A. | y=-x | B. | y=-$\frac{3}{4}$x | C. | y=-$\frac{3}{5}$x | D. | y=-$\frac{9}{10}$x |
| A. | $\frac{15}{2}$ | B. | 15 | C. | -$\frac{15}{2}$ | D. | -15 |
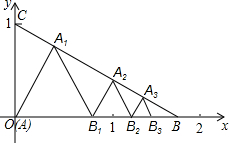 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{n}}$ | B. | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C. | $\frac{3}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n-1}}$ |
 一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )
一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是( )| A. | 和 | B. | 谐 | C. | 泰 | D. | 州 |
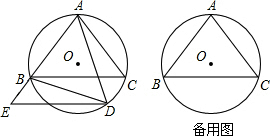 如图,⊙O是△ABC的外接圆,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD,且∠ADB=∠E.
如图,⊙O是△ABC的外接圆,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD,且∠ADB=∠E.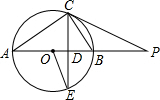 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.