题目内容
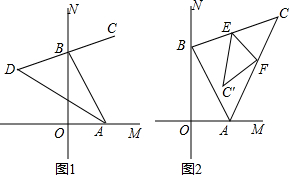
4. 如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE
如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE求证:(1)AE=CF;
(2)AE∥CF
(3)∠AFE=∠CEF.
分析 (1)易证BE=DF,即可求证△ABE≌△CDF,即可解题;
(2)根据(1)中的△ABE≌△CDF可得∠AEB=∠CFD,即可解题
(3)根据全等三角形的性质得到∠AFB=∠DEC,根据邻补角的定义即可得到结论.
解答 解:(1)∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{BE=DF}\\{∠B=∠D}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴AE=CF;
(2)由(1)知:△ABE≌△CDF,
∴∠AEB=∠CFD,
∴AE∥CF;
(3)在△ABF和△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠D}\\{BF=DE}\end{array}\right.$,
∴△ABF≌△CDE(SAS),
∴∠AFB=∠DEC,
∴∠AFE=∠CEF.
点评 本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABE≌△CDF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.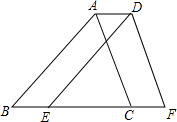 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )| A. | 2:1 | B. | 3:2 | C. | 4:3 | D. | 不能确定 |

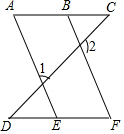 如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:
如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说: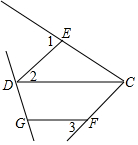 如图,已知∠1=∠ECF,∠2=∠3,那么∠GDC+∠DGF=180°吗?请说明理由.
如图,已知∠1=∠ECF,∠2=∠3,那么∠GDC+∠DGF=180°吗?请说明理由.