题目内容
11．求一个一元二次方程，使它的两根分别是方程5x2+2x-3=0的各根的负倒数．分析 设方程5x2+2x-3两个为x1，x2，根据根与系数的关系得到x1+x2=-$\frac{2}{5}$，x1•x2=-$\frac{3}{5}$，再分别计算-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$和-$\frac{1}{{x}_{1}}$•（-$\frac{1}{{x}_{2}}$），然后根据根与系数的关系写出以-$\frac{1}{{x}_{1}}$和-$\frac{1}{{x}_{2}}$为两根的一元二次方程．
解答 解：设方程5x2+2x-3两个为x1，x2，
则x1+x2=-$\frac{2}{5}$，x1•x2=-$\frac{3}{5}$，
-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{2}{3}$和-$\frac{1}{{x}_{1}}$•（-$\frac{1}{{x}_{2}}$）=$\frac{1}{{x}_{1}{x}_{2}}$=-$\frac{5}{3}$，
所以以-$\frac{1}{{x}_{1}}$和-$\frac{1}{{x}_{2}}$为两根的一元二次方程为x2+$\frac{2}{3}$x-$\frac{5}{3}$=0．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
阅读快车系列答案
相关题目
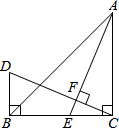在△ABC中，∠ACB=90°，E是BC边上的一点，过C作CF⊥AE，垂足为F，过点B作BD⊥BC，交CF的延长线于点D，若∠D=65°，求∠EAC的度数．
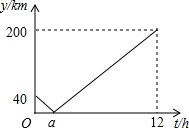甲、乙两车要从M地沿同一条公路运输一批物资到N地，乙车比甲车先行驶1h，设甲车与乙车之间的距离为y（单位：km），甲车行驶时间为t（单位：h），y与t之间的函数关系如图所示（假设甲、乙两车速度始终保持不变）．结合图象解答下列问题：