题目内容

20．x为整数，且满足5x-$\frac{5}{7}$＞4x+7与8x-3＜4x+50，则整数x=8，9，10，11，12，13．．

分析 首先解两个不等式求得x的范围，然后求得在此范围内的整数即可．

解答 解：解不等式5x-$\frac{5}{7}$＞4x+7得：x＞$\frac{54}{7}$；
解不等式8x-3＜4x+50，得：x＜$\frac{53}{4}$，
则整数x是：8，9，10，11，12，13．
故答案为8，9，10，11，12，13．

点评 此题考查的是一元一次不等式的解法和一元一次方程的解，根据x的取值范围，得出x的整数解，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
15．下列不等式变形正确的是（　　）
A．由4x-1≥0得4x＞1B．由3x＞0得x＞-3C．由-2x＜4得x＜-2D．由$\frac{y}{2}$≥0得y≥0
11．问题提出
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而“作差法”就是常用的解决问题的策略之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小．
（1）利用“作差法”解决问题
如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，设两个小正方形面积之和为M，两个矩形面积之和为N，试比较M与N的大小．
（2）类比应用
①已知甲、乙两人的速度分别是V甲=$\frac{x+y}{2}$千米/小时、V乙=$\frac{2xy}{x+y}$千米/小时（x、y是正数，且x≠y），试比较V甲、V乙的大小．
②如图2，在边长为a的正方形ABCD中，以A为圆心，$\frac{3}{4}a$为半径画弧交AB、AD于点E、F，以CD为直径画弧，若图中阴影部分的面积分别为S1，S2，试比较S1与S2的大小．
8．在数轴上A、B两点表示的数分别为-1和$\sqrt{3}$，点B关于点A的对称点为C，则点C表示的数为-2-$\sqrt{3}$；若在此数轴上与点A距离等于5的为点D，则点D表示的数为4或-6．
15．若两个最简二次根式$\sqrt{2a}$与$\sqrt{9-a}$可以合并，则a=3．
5．写出以$4+\sqrt{17}、4-\sqrt{17}$为两根的关于x的一元二次方程x2-8x-1=0．
12．①m2-6m-9991=0；          
②2x2-5x=1；          
③9（2a-5）2=16（3a-1）2
④（x2-5）2-3（x2-5）-4=0；                  
⑤x2-2|x-1|-1=0．
9．已知关于x的分式方程$\frac{x}{x-2}$=$\frac{a}{x-2}$+2无解，求关于y的不等式$\frac{ay-1}{3}$-$\frac{9y+a}{6}$≤1的解集，并在数轴上把解集表示出来．
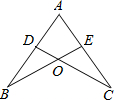10．如图，已知点D在AB上，点E在AC上，AB=AC，请你再补充一个条件，使△ABE≌△ACD．你补充的条件是∠B=∠C或AD=AE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网