题目内容
阅读材料:设方程ax2+bx+c=0(a≠0)的两根为x1、x2,则两根与方程系数之间有如下关系:x1+x2=-
,x1•x2=
.根据该材料填空:若关于x的一元二次方程x2-(n+2)x-2n2=0的两根记作an、bn(n为不小于2的整数),则
+
+…+
= .
| b |
| a |
| c |
| a |
| 1 |
| (a2-2)(b2-2) |
| 1 |
| (a3-2)(b3-2) |
| 1 |
| (an-2)(bn-2) |
考点:根与系数的关系
专题:
分析:首先根据两根与方程系数之间的关系求得an+bn=n+2,an•bn=-2n2,然后由
=-
(
-
)找到规律原式=-
(
-
+
-
+…+
-
)=-
(
-
)=-
.
| 1 |
| (an-2)(bn-2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| n-1 |
| 4(n+1) |
解答:解:∵关于x的一元二次方程x2-(n+2)x-2n2=0的两根记作an、bn(n为不小于2的整数),
∴an+bn=n+2,an•bn=-2n2,
∴
=
=
=-
•
=-
(
-
),
∴
+
…+
=-
(
-
+
-
+…+
-
)=-
(
-
)=-
;
故答案是:-
.
∴an+bn=n+2,an•bn=-2n2,
∴
| 1 |
| (an-2)(bn-2) |
| 1 |
| anbn-2(an+bn)+4 |
| 1 |
| -2n2-2n |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| (a2-2)(b2-2) |
| 1 |
| (a3-2)(b3-2) |
| 1 |
| (an-2)(bn-2) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| n-1 |
| 4(n+1) |
故答案是:-
| n-1 |
| 4(n+1) |
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
设a=
-1,则代数式a2+2a-10的值为( )
| 7 |
| A、-3 | ||
| B、-4 | ||
C、-4
| ||
D、-4
|
方程(3x-1)(2x+4)=1的解是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 图所示),已知AD∥BC,∠B=90°,设AB=x,且AB<BC,其余两边用10米长的建筑材料修建,恰好用完.
图所示),已知AD∥BC,∠B=90°,设AB=x,且AB<BC,其余两边用10米长的建筑材料修建,恰好用完. 已知等腰梯形ABCD中,A (-3,0),B (4,0),C (2,2),一条直线y=-
已知等腰梯形ABCD中,A (-3,0),B (4,0),C (2,2),一条直线y=-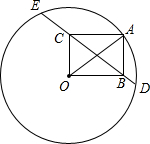 如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是
如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是 如图,矩形OABC边OA长为1,边AB长为2,OC在数轴上,且点O与原点重合.以O为圆心,对角线OB的长为半径画弧,交负半轴于点D,则点D表示的实数是( )
如图,矩形OABC边OA长为1,边AB长为2,OC在数轴上,且点O与原点重合.以O为圆心,对角线OB的长为半径画弧,交负半轴于点D,则点D表示的实数是( )