题目内容
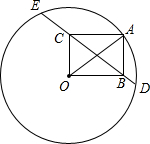如图所示，点A在半径为20的圆O上，以OA为一条对角线作矩形OBAC，设直线BC交圆O于D、E两点，若OC=12，则线段CE、BD的长度差是考点：垂径定理,勾股定理
专题：探究型
分析：设DE的中点为M，连接OM，则OM⊥DE，在Rt△AOB中利用勾股定理求出OB的长，利用三角形的面积公式求出OM的长，在Rt△OCM中，利用勾股定理求出CM的长，进而可得出BM的长，由CE-BD=（EM-CM）-（DM-BM）=BM-CM即可得出结论．
解答：
解：如图，设DE的中点为M，连接OM，则OM⊥DE．
∵在Rt△AOB中，OA=20，AB=OC=12，
∴OB=
=
=16，
∴OM=
=
=
，
在Rt△OCM中，
CM=
=
=
，
∵BM=BC-CM=20-
=
，
∴CE-BD=（EM-CM）-（DM-BM）=BM-CM=
-
=
．
故答案为：
．
解：如图，设DE的中点为M，连接OM，则OM⊥DE．∵在Rt△AOB中，OA=20，AB=OC=12，
∴OB=
| OA2-AB2 |
| 202-122 |
∴OM=
| OB•OC |
| BC |
| 16×12 |
| 20 |
| 48 |
| 5 |
在Rt△OCM中，
CM=
| OC2-OM2 |
122-(
|
| 36 |
| 5 |
∵BM=BC-CM=20-
| 36 |
| 5 |
| 64 |
| 5 |
∴CE-BD=（EM-CM）-（DM-BM）=BM-CM=
| 64 |
| 5 |
| 36 |
| 5 |
| 28 |
| 5 |
故答案为：
| 28 |
| 5 |
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理进行解答是解答此题的关键．
练习册系列答案
相关题目
正方形ABCD中，点E在DC延长线上，点F在CB延长线上，∠EAF=45°，∠BAF=15°5-1的倒数是（ ）
| A、5 | ||
B、-
| ||
C、
| ||
| D、-5 |
规作图确定医院M的位置．（不要求写出作法、证明，但要保留作图痕迹，请务必用铅笔作图）．
如图，△ABC内接于⊙O，AD是BC边上的高，AO的延长线交⊙O于点E．已知AB=| 6 |
| 3 |
A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
如图，正方形ABCD的面积是120平方厘米，E是AB的中点，F是BC的中点，四边形BGHF的面积是多少平方厘米？
如图，在?ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠C=∠EFB．