Question

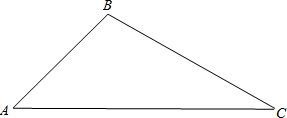
已知等腰梯形ABCD中，A （-3，0），B （4，0），C （2，2），一条直线y=-

3

2

x+b将梯形ABCD面积等分，则b=

 

．

Answer 1

考点：一次函数综合题

专题：计算题,压轴题

分析：过点C作CE⊥AB于E，作DF⊥AB于F，根据梯形ABCD是等腰梯形，得到AD=BC，∠DAF=∠CBE，从而推出△ADF≌△BCE，根据全等三角形的性质求出AF=BE，可以得到A、B、C的坐标，再根据等腰梯形及矩形的性质求出D点坐标，求出直线与梯形上下底的交点坐标（含字母b），将梯形分为DAMN和CNMB两个梯形，建立等式即可．

解答：解：过点C作CE⊥AB于E，作DF⊥AB于F，
∴∠DFA=∠CEB=90°，
∵梯形ABCD是等腰梯形，
∴AD=BC，∠DAF=∠CBE，
在△ADF和△BCE中，

∠DAF=∠CBE ∠DFA=∠CEB AD=BC

，
∴△ADF≌△BCE（AAS），
∴AF=BE，
∵A（-3，0），B（4，0），C（2，2），
∴AB=7，BE=2，OA=3，CE=DF=2，
∴AF=2，
∴OF=1，
∴点D（-1，2），
∴CD=3，
∴S_梯形ABCD=

1

2

（AB+CD）×CE=

1

2

×（3+7）×2=10，
设直线y=-

3

2

x+b与梯形ABCD分别交于点M，N，
∴点M（

2

3

b，0），点N（

2

3

（b-2），2），
∴S_梯形DAMN=

2{[ 2 3 (b-2)+1]+( 2 3 b+3)}

2

，
S_梯形CNMB=

2{(4- 2 3 b)+[2- 2 3 (b-2)]}

2

，
∴

2{[ 2 3 (b-2)+1]+( 2 3 b+3)}

2

=

2{(4- 2 3 b)+[2- 2 3 (b-2)]}

2

，
解得，b=

7

4

．
故答案为

7

4

．

点评：本题考查了一次函数的性质和等腰梯形的性质，求出直线与梯形上、下底的交点坐标，将梯形分为两个梯形是解题的关键．