题目内容
10.若t=2-$\sqrt{-3{x}^{2}+12x-9}$,则t的最大值为2,最小值为2-$\sqrt{3}$.分析 首先求得-3x2+12x-9的最大值,从而得到$\sqrt{-3{x}^{2}+12x-9}$的取值范围,然后可确定出t的最大值和最小值.
解答 解:由二次函数的顶点坐标公式可知:-3x2+12x-9的最大值为3,
∴0≤$\sqrt{-3{x}^{2}+12x-9}$≤$\sqrt{3}$.
∴t的最大值为2,最小值为2-$\sqrt{3}$.
故答案为:2;2-$\sqrt{3}$.
点评 本题主要考查的是二次函数的最值,求得$\sqrt{-3{x}^{2}+12x-9}$的取值范围是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
18.计算:(2xy2)4•(-6x2y)÷(-12x3y2)的结果为( )
| A. | 16x3y7 | B. | 4x3y7 | C. | 8x3y7 | D. | 8x2y7 |
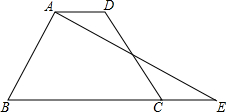 如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.
如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.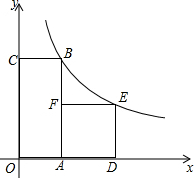 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4. 如图,在平面直角坐标系中,圆P(以点P为圆心的圆)上有两个点A(7,0)、B(3,-4),将圆P平移,使圆心P(5,-2)平移到点P′(-3,3)
如图,在平面直角坐标系中,圆P(以点P为圆心的圆)上有两个点A(7,0)、B(3,-4),将圆P平移,使圆心P(5,-2)平移到点P′(-3,3)